Дано: рівняння кривої другого порядку \( 9x^2 - 49y^2 + 18x - 490y-775 = 0 \)
1. Запишемо рівняння кривої в канонічному вигляді.
В даному рівнянні є тільки члени другого і першого ступеня (немає змішаного добутку), тому канонічне рівняння будемо отримувати методом виділення повного квадрата.
$$ 9x^2 - 49y^2 + 18x- 490y-775 = 0 = > $$$$ 9 (x^2 + 2x) -49 (y^2 + 10y) -775 = 0 = > $$ доповнюємо члени в дужках до повного квадрата $$ 9 (x^2 + 2x + 1-1) -49 (y^2 + 2 * 5y + 25-25) -775 = 0 = > $$$$ 9 (x + 1)^2 -49 (y + 5)^2 + 441 = 0 = > $$$$ -9 (x + 1)^2 + 49 (y + 5 )^2 = 441 = > $$ розділимо обидві частини рівняння на 441 $$ - \frac{(x + 1)^2}{49} + \frac{(y + 5)^2}{9} = 1 = > \quad (1) $$
Отримали рівняння гіперболи.
Розглянемо канонічне рівняння гіперболи $$ \frac{y^2}{b^2} - \frac{x^2}{a^2} = 1 $$ знак мінус стоїть перед змінної x, це означає, що дійсна вісь - вісь Oy, уявна вісь - вісь Ox. Вершини гіперболи лежать га вісь Oy симетрично відносно початку координат.
Для того, щоб привести рівняння (1) до канонічного виду введемо нові координати \(x'= x + 1; y' = y + 5 \), підставляємо в рівняння (1) і отримуємо канонічне рівняння гіперболи в новій системі координат (x'; y'), яка зміщена щодо базової системи координат на по осі Оx вліво на 1 і по осі Оy вниз на 5, отримуємо $$ \frac{(y')^2}{9} - \frac{(x')^2}{49} = 1 $$
2. Знайдемо півосі гіперболи:
Канонічне рівняння гіперболи має вигляд \( \frac{y^2}{b^2} - \frac{x^2}{a^2} = 1 \), де \(a\) і \(b\) - півосі гіперболи, тобто \(a = 7; \quad b = 3 \),
\(a = 7 \) - уявна піввісь
\(b = 3 \) - дійсна піввісь
Відповідь : півосі гіперболи дорівнюють \(a = 7; \quad b = 3 \)
3. Знайдемо координати вершин гіперболи.
Вершини гіперболи - точки перетину гіперболи з дійсною віссю. Дійсна вісь -ось Oy і гіпербола симетрична щодо осі Ox, тому координати вершин \(A_1 (0; -b); A_2 (0; b) \), де \(b = 3 \) - дійсна піввісь.
Дані координати для системи координат \((x'; y') \), повертаємося до базових координатам \( x'= x + 1; y' = y + 5 = > x = x'-1; y = y'-5 \), координати вершин в базовій системі координат \(A_1 (-1; -b-5); A_2 (-1; b-5) \), одержуємо \(A_1 (-1; -8); A_2 (-1; -2) \)
Відповідь : координати вершин в базовій системі координат \(A_1 (-1; -8); A_2 (-1; -2) \)
4. Знайдемо координати фокусів гіперболи:
Для знаходження координат фокусів, скористаємося співвідношенням, що зв'язує піввісь і фокусна відстань \(c^2 = a^2 + b^2 \), підставляємо значення \(c^2 = 7^2 + 3^2 = > c = \sqrt{58} \approx 7.6 \). Координати фокусів для гіперболи, заданої в канонічному вигляді, наступні з дійсною віссю Oy \(F_1 (0; -c); F_2 (0; c) \)
Дані координати для системи координат \((x'; y') \), повертаємося до базових координатам \( x'= x + 1; y' = y + 5 = > x = x' -1; y = y'-5 \), координати фокусів у базовій системі координат \(F_1 (-1; -c-5); F_2 (-1; c-5) \), одержуємо \(F_1 ( -1; -12.6); F_2 (-1; 2.6) \)
Відповідь : координати фокусів гіперболи в базовій системі координат \(F_1 (-1; -12.6); F_2 (-1; 2.6) \)
5.Найдем асимптоти гіперболи:
Рівняння асимптот мають вигляд \(y = \pm \frac{b}{a} x \). Підставляємо дані і отримувати дві асимптоти в новій системі координат \(y'= \frac{3}{7} x'; \quad y'= - \frac{3}{7} x' \)
Дані координати для системи координат \((x'; y') \), повертаємося до базових координатам \( x'= x + 1; y' = y + 5 \), рівняння асимптот матимуть вигляд, $$ y + 5 = \frac{3}{7} (x + 1); \quad y + 5 = - \frac{3}{7} (x + 1) = > $$$$ y = \frac{3}{7} x - \frac{32}{7} \quad y = - \frac{3}{7} x - \frac{38}{7} $$
Відповідь : рівняння асимптот гіперболи \( y = \frac{3}{7} x - \frac{32}{7} \quad y = - \frac{3}{7} x - \frac{38}{7} \)
6. Знайдемо ексцентриситет гіперболи:
Ексцентриситет гіперболи будемо шукати за формулою $$ \epsilon = \frac{c}{a} = \sqrt{1+ (\frac{b}{a})^2} $$ підставляємо дані $$ \epsilon = \frac{\sqrt{58}}{7} $$
Відповідь : ексцентриситет гіперболи \( \epsilon = \frac{\sqrt{58}}{7} \)
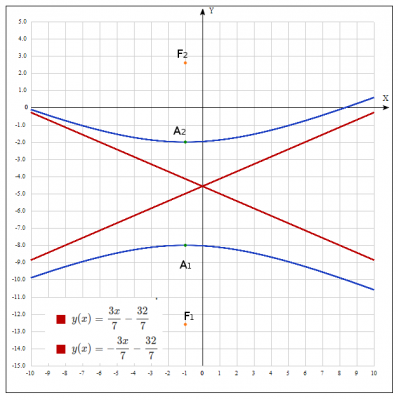
7. Малюнок: