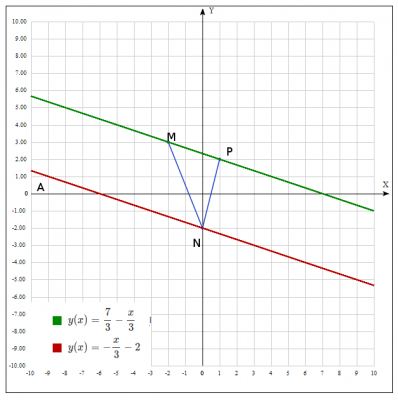
Рішення : знайдемо рівняння прямої (назвемо її NA), що проходить через задану точку \(N (0; -2)\) паралельно стороні \(MP\) для цього скористаємося рівнянням прямий яка роходить через задану точку в заданому напрямку $$ y - y_0 = k (x - x_0)\quad (1) $$
З умови задачі одержуємо, що в рівнянні (1) відомі координати \((x_0; y_0 )\) - координати вершини \(N (0; -2)\).
Необхідно знайти кутовий коефіцієнт \(k\).
З умови відомо, що дві прямі паралельні. Скористаємося властивістю кутових коефіцієнтів паралельних прямих \(k_1 = k_2\)
Знайдемо кутовий коефіцієнт прямої, на якої лежить сторона \(MP\)
Рівняння стороони \(MP\) трикутника.
Дано координати двох вершини трикутника \(M (-2; 3); P (1; 2)\), тому рівняння сторони будемо шукати за допомогою формули рівняння прямої, що проходить через дві задані точки \(\frac{ x-x_1}{x_2-x_1} =\frac{y-y_1}{y_2-y_1} \quad (1)\) Підставляємо координати вершин:
рівняння сторони \(MP\), при відомих координатах вершини \(M (-2; 3); P (1; 2)\) $$ MP \quad \frac{x + 2}{1 + 2} =\frac{y-3}{2-3 } => y =\frac{7}{3} -\frac{1}{3} x \quad (2) $$
Відповідь : рівняння сторони \(MP\):\(y =\frac{7}{3} -\frac{1}{3} x\)
З отриманого рівняння (2) визначаємо кутовий коефіцієнт \(k = -\frac{1}{3}\)
Рівняння прямої \(NA\).
Підставляємо координати точки \(N (0; -2)\) і значення кутового коефіцієнта \(k = -\frac{1}{3}\) в рівняння прямої (1), це і буде шукане рівняння прямої NA, що проходить через точку N паралельно стороні MP:
$$ NA:\quad y + 2 = -\frac{1}{3} (x - 0) => y = -\frac{1}{3} x - 2 $$
Відповідь : рівняння прямої \(NA \quad y = -\frac{1}{3} x - 2\)