Решение: применим второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: $$ \vec{F} = m\vec{a}$$
Если на тело одновременно действуют несколько сил (например, \(\vec{F_1};\vec{F_2},\vec{F_3}\), то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил: $$\vec{F} = \vec{F_1}+\vec{F_2}+\vec{F_3} => \sum \vec{F} = m\vec{a}$$
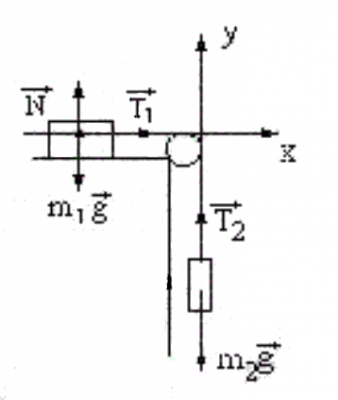
Запишем второй закон Ньютона для тележки (см.рис.) $$ \vec{N}+\vec{T_1}+m_1\vec{g} = m_1\vec{a}$$
Запишем второй закон Ньютона для гири (см.рис.) $$ \vec{T_2}+m_2\vec{g} = m_2\vec{a}$$ Составим систему уравнений $$ \begin{cases} \vec{N}+\vec{T_1}+m_1\vec{g} = m_1\vec{a}\\\vec{T_2}+m_2\vec{g} = m_2\vec{a} \end{cases} => $$ перейдем к проекциям сил на оси $$ \begin{cases} N + T_1 - m_1g = m_1a \\ T_2 - m_2g = -m_2a \end{cases} => $$ Сила тяжести \(m_1\vec{g}\) и сила реакции опоры \( \vec{N}\) равны между собой и противонаправлены, т.е. \( \vec{N}+m_1\vec{g} => N -m_1g =0\), получаем
$$ \begin{cases} T_1 = m_1a \\ T_2 - m_2g = -m_2a \end{cases} => $$ Учтем, что \(T_1=T_2=T\), получаем $$ \begin{cases} T = m_1a \\ T - m_2g = -m_2a \end{cases} => \begin{cases} T = m_1a \\ m_1a - m_2g = -m_2a \end{cases} =>$$$$ \begin{cases} T = m_1a \\ a = \frac{m_2g}{m_2+m_1} \end{cases} $$ Подствляем данные и находим ускорение $$ a = \frac{m_2g}{m_2+m_1} = \frac{2*9.8}{1+2} \approx 6.53$$
Определим работу силы тяжести, действующей на гирю на пути 10см
Работой A, совершаемой постоянной силой \(\vec{F}\), называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы \(\vec{F}\) и перемещения \(\vec{s}\) $$A = Fs\cos(\alpha)$$ Подставляем данные в формулу, учтем,что \( α = 0 => \cos(\alpha) = 1\), получаем $$ A = Fs = m_1a*s = 1*6.53*0.1 = 0.653Дж$$