–†–µ—И–µ–љ–Є–µ: –і–ї—П —А–µ—И–µ–љ–Є—П –њ—А–Є–Љ–µ–љ–Є–Љ —Д–Њ—А–Љ—Г–ї—Г —Г—А–∞–≤–љ–µ–љ–Є—П –њ—А—П–Љ–Њ–є –≤ –Њ—В—А–µ–Ј–Ї–∞—Е –љ–∞ –Њ—Б—П—Е $$ \frac{x}{a} + \frac{y}{b} = 1 \quad (1)$$ –≥–і–µ
\(a\) - –Њ—В—А–µ–Ј–Њ–Ї, –Ї–Њ—В–Њ—А—Л–є –Њ—В—Б–µ–Ї–∞–µ—В –њ—А—П–Љ–∞—П –Њ—В –Њ—Б–Є Ox,
\(b\) - –Њ—В—А–µ–Ј–Њ–Ї, –Ї–Њ—В–Њ—А—Л–є –Њ—В—Б–µ–Ї–∞–µ—В –њ—А—П–Љ–∞—П –Њ—В –Њ—Б–Є Oy.
–Ш–Ј —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є —Б–ї–µ–і—Г–µ—В, –Њ—В—А–µ–Ј–Њ–Ї, –Ї–Њ—В–Њ—А—Л–є –њ—А—П–Љ–∞—П –Њ—В—Б–µ–Ї–∞–µ—В –Њ—В –Њ—Б–Є Ox - –Њ—В—А–µ–Ј–Њ–Ї \(a\), –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ, —З–µ–Љ –љ–∞ –Њ—Б–Є Oy - –Њ—В—А–µ–Ј–Њ–Ї \(b\), —В.–µ \(a = 2b => b=\frac{1}{2}a\).
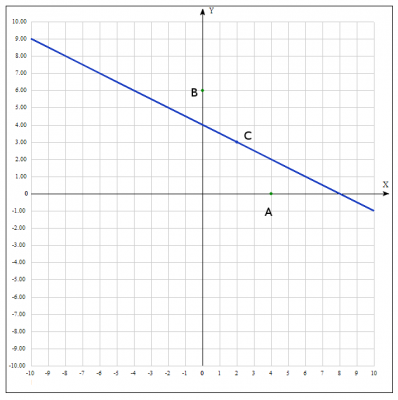
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ (1) $$ \frac{x}{a} + \frac{y}{b} = 1 => \frac{x}{a} + 2\frac{y}{a} = 1 \quad (2)$$ –Э–∞–є–і–µ–Љ –љ–µ–Є–Ј–≤–µ—Б—В–љ—Г—О \(a\). –Ф–ї—П —Н—В–Њ–≥–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –≤—В–Њ—А–Њ–є —З–∞—Б—В—М—О —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є - –Є—Б–Ї–Њ–Љ–∞—П –њ—А—П–Љ–∞—П –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ AB, —Г –Ї–Њ—В–Њ—А–Њ–≥–Њ –Є–Ј–≤–µ—Б—В–љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–µ–Ї A (4;0) –Є B (0;6). –Ъ–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–Ї–Є —Б–µ—А–µ–і–Є–љ—Л –Њ—В—А–µ–Ј–Ї–∞ –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$( \frac{x_A+x_B}{2};\frac{y_A+y_B}{2}) \quad (3)$$ –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Ї–Њ–љ—Ж–Њ–≤ –Њ—В—А–µ–Ј–Ї–∞ –≤ —Д–Њ—А–Љ—Г–ї—Г (3) –Є –љ–∞–є–і–µ–Љ –Є—Б–Ї–Њ–Љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л $$ C( \frac{4+0}{2};\frac{0+6}{2}) => C(2; 3)$$ –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ (2) $$ \frac{2}{a} + 2\frac{3}{a} = 1 => a= 8 => b=4$$ –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Ј–љ–∞—З–µ–љ–Є—П \(a;b\) –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ (1), –њ–Њ–ї—Г—З–∞–µ–Љ –Є—Б–Ї–Њ–Љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ $$ \frac{x}{8} + \frac{y}{4} = 1 => y = 4-\frac{1}{2}x$$
–Ю—В–≤–µ—В: —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є \( y = 4-\frac{1}{2}x\)