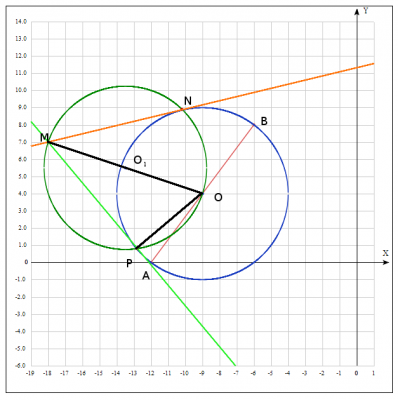
Дано точки A (-12; 0) і B (-6; 8).
Знайти:
1 .Рівняння кола, діаметром якого є відрізок AB,
2. Рівняння дотичних до кола, проведених із точки M (-18; 7).
Рішення:
розглянемо канонічне рівняння кола $$ (x-x_1)^2 + (y-y_1)^2 = R^2 \quad (1) $$ де координати \(O (x_1; y_1) \) - координати центру кола.
1. Знайдемо радіус кола.
Відповідно до умови завдання, відрізок \(AB \) - діаметр окружності, знайдемо його за формулою відстані між двома точками \(d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 } \). Підставляємо координати точок $$ d = 2R = \sqrt{(- 6 + 12)^2 + (8-0)^2} = 10 = > R = 5 $$
2. Знайдемо координати центру кола \(O (x_1; y_1) \)
центр кола лежить по середині відрізка \(AB \). Середину відрізка будемо шукати за формулою \(O (\frac{x_2 + x_1}{2}; \frac{y_2 + y_1}{2}) \quad (2) \).
Підставляємо координати точок A (-12; 0) і (-6; 8), отримуємо $$ O (\frac{-12-6}{2}; \frac{0 + 8}{2}) = > O (-9; 4) $$
3. Рівняння кола.
Підставляємо, отримані дані в рівняння кола (1), отримуємо $$ (x + 9)^2 + (y-4)^2 = 5^2 $$
4. Знайдемо рівняння дотичних до кола з точки M (-18; 7).
Можна застосувати рівняння дотичної $$ y = f (x_0) + f '(x_0) (x-x_0) $$
В даному випадку вирішимо інакше.
Проведемо побудови:
4.1. З'єднаємо точку М з центром кола О.
4.2. Побудуємо дотичну (потрібен малюнок, щоб розуміти рішення).
4.3. Опустимо радіус в точку дотику, він буде перпендикулярний дотичній.
Всі ці побудови потрібні, щоб побудувати коло з центром посередині відрізка МО - точка \(O_1 \) і радіусом рівним половині довжини відрізка МО, тоді точки дотику - точки перетину кіл.
4.4. Координати центру кола знайдемо за формулою (2) \(O_1 (\frac{-18-9}{2}; \frac{4 + 7}{2}) = > O_1 (- \frac{27}{ 2}; \frac{11}{2}) \)
4.5 знайдемо радіус кола за формулою відстані між точками \(d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \), одержуємо $$ d = 2R = \sqrt{(- 18 + 9)^2 + (7-4)^2} = > R = \frac{\sqrt{90}}{2} $$
4.6. Отримали рівняння другого окружності $$ (x + \frac{27}{2})^2 + (y - \frac{11}{2})^2 = 22.5 $$
4.7. Складаємо систему рівнянь у складі двох рівнянь кіл, вирішуємо його і знаходимо координати точок перетину кіл (дотичних)
$$ \begin{cases} (x + 9)^2 + (y-4)^2 = 5^2 \\ (x + \frac{27}{2})^2 + (y - \frac{11}{2})^2 = 22.5 \end{cases} = > \begin{cases} x_1 \approx -12.8 ; & x_2 \approx -10.2 \\ y_1 \approx 0.8; & y_2 \approx 8,9 \end{cases} $$
Отримали координати точок дотику.
4.8. Складемо рівняння дотичних до кола, проведених із заданої точки.
Для рівнянь дотичних нам відомі по дві точки. Застосуємо формулу прямої, що проходить через дві задані точки $$ \frac{x - x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (4) $$
Підставляємо координати точок :
перше рівняння дотичній для точок M (-18; 7) і P(-12.8; 0.8): $$ \frac{x + 18}{- 12.8 + 18} = \frac{y- 7}{0.8-7} = > y = -1.19x-14.42 $$
друге рівняння дотичній для точок M (-18; 7) і N(-10.2; 8.9): $$ \frac{x + 18}{- 10.2 + 18} = \frac{y-7}{8.9-7} = > y = 0.24x + 11.32 $$