Запишем уравнение параболы, ось которой параллельна оси \(Oy\) $$(x-x_0)^2 = 2p(y-y_0)$$где \((x_0;y_0)\) - вершина параболы. Она известна, подставим координаты вершины в уравнение и получим $$(x-2)^2 = 2p(y+16)$$в уравнении остался неизвестен параметр параболы \(p\), для его нахождения будем использовать вторую точку в условии с координатами \((3;-15)\), которая принадлежит параболе и найдем параметр \(p\). $$(x-2)^2 = 2p(y+16) => (3-2)^2 = 2p(-15+16) =>1 = 2p =>p =\frac{1}{2}$$получили параметр \(p>0\) это говорит то, что оси параболы направлены вверх. Получили уравнение параболы $$(x-2)^2 = y+16$$
Найдем точки пересечения с осью абсцисс \(Ox\) - точки, у которых \(y =0\). Подставим в уравнение и получим $$(x-2)^2 = y+16 => (x-2)^2 = 16$ => x^2 - 4x -12 = 0 => x_1=6; x_2=-2$$Получили две точки пересечения с осью \(Ox\) это \((6;0),(-2;0)\).
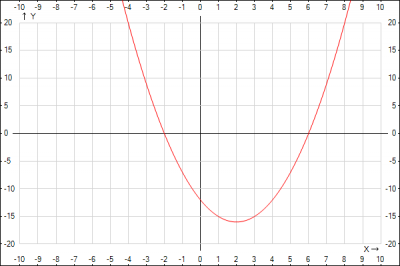
Построим параболу по полученным данным