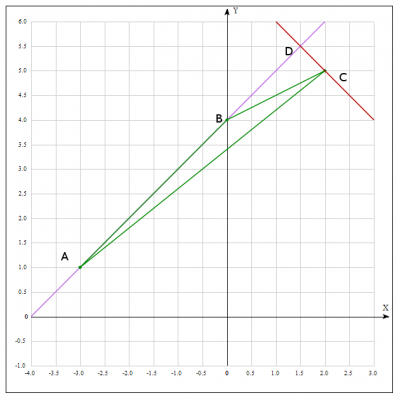
Даны вершины треугольника АВС: А(-3, 1), В(0, 4), С(2, 5).
Написать уравнение высоты, проведенной из вершины С к стороне АВ.
Уравнение высоты \(CD\), опущенной из вершины \(C\) на сторону \(AB\).
Высота \(CD\) опущена из вершины \(C\) на сторону \(AB\), т.е. из условия известна одна координата точки \(C(2;5)\) и направление - прямая перпендикулярна прямой \(AB\).
Воспользуемся свойством угловых коэффициентов перпендикулярных прямых: \(k_1 = -\frac{1}{k_2}\). Найдем угловой коэффициент прямой стороны \(AB\).
Уравнения стороны будем искать при помощи формулы уравнения прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \) Подставляем координаты вершин:
уравнение стороны \(AB\), при известных координатах вершины \(А(-3;1), B(0;4)\) $$ AC \quad \frac{x+3}{0+3} = \frac{y-1}{4-1} => y = x +4$$
Ответ: уравнение стороны \(AB\): \(y = x + 4\)
Получили \( k_{AB} = 1 =>\) \( k_{CD} = -\frac{1}{AB} = -1\). Найдем уравнение прямой \(CD\), для этого воспользуемся уравнением прямой проходящей через заданную точку \(C(2;5)\) в заданном направлении \( k_{CD} = -1\) $$ y - y_0 = k(x - x_0) \quad (2)$$ получим $$ y - 5 = - 1(x - 2) => y = -x+7$$
Ответ: уравнение высоты \(CD\): \( y = -x+7 \)