Рішення :
Метод відстаней.
Знайдемо геометричній місце точок, що задовольняє заданій умові. Нехай точка з координатами A (x; y) задовольняє цим умовам.
Відстань від точки A (x; y) до прямої \(x-4 = 0 = > x = 4 \) дорівнює \(d = | x-4 | \)
Відстань від точки A (x; y) до точки \(M_0 (9; 0) \) дорівнює \(d = \sqrt {(x-9)^2 + y^2} \)
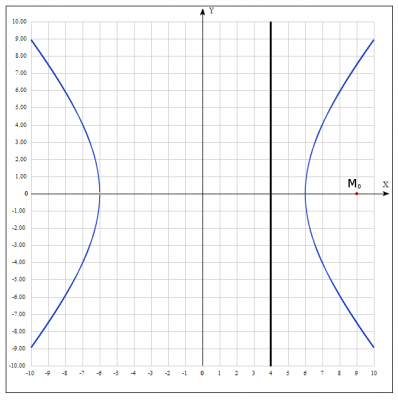
Згідно умови задачі, ставлення цих відстаней одно \( \frac {3} {2} \), одержуємо $$ \frac {\sqrt {(x-9) ^ 2 + y ^ 2}} { | x-4 |} = \frac {3} {2} = > \frac{ (x-9)^2 + y^2} { ( x-4)^2} = \frac{9}{4} = > $$$$ 4 (x-9)^2 + 4y^2 = 9 (x-4)^2 = > $$$$ 4x^2 -72x + 324 + 4y^2 = 9x^2 -72x + 144 => $$$$ 180 = 5x^2 -4y^2 => \frac{x^2}{36} - \frac{y^2} {45} = 1 $$ Отримали рівняння гіперболи.
Перевірка результатів.
Для перевірки, виберемо будь-яку точку гіперболи і порівняємо відстань від гіперболи до директриси і фокусу.
Нехай \(x = 6 => y = 0 \). Отримали точку з координатами \((6; 0) \).
Відстань від точки до директриси - прямий \(x = 4 \) одно \(d_1 = 6-4 = 2 \) .
Відстань від точки до фокусу \(M_0 (9; 0) \) знайдемо за формулою відстані між точками \(d = \sqrt {(x_2-x_1)^2 + (y_2-y_1)^2} \), одержуємо \(d_2 = \sqrt{(9-6)^2 + (0-0)^2} = 3 \)
Знайдемо відношення цих відстаней \( \frac{d_2}{d_1} = \frac{3}{2} \)
Побудуємо параболу і переконаємося в правильності рішення.