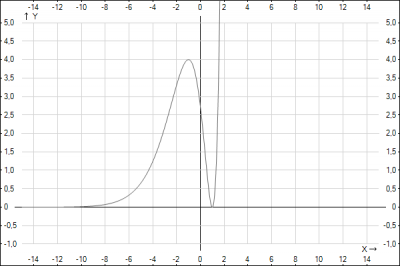
Проведем исследование и построим график функции \(y=(x-1)^2 e^{x+1}\). Исследование будем проводить согласно общей схемы исследования функции и построения графика функции.
Приступаем.
1. Определим область определения функции. Данная функция сложная, состоит из многочлена первой степени и показательной функции. Каких-либо ограничений по области определения у них нет, поэтому область определения общей функции будет $$D_f = R$$
2. Определим область значения функции. Область значения функции \(y = (x-1)^2\) \(E_f = [0; +\infty)\), область значения функции \(y = e^{x+1}\) \(E_f = (0; +\infty)\),т.о. область значения заданной функции \(y=(x-1)^2 e^{x+1}\) $$E_f = (0; +\infty)$$
3. Найдем точки пересечения с осями.
3.1. Точки пересечения с осью \(Ox\). Это точки у которых \(y = 0\). Приравняем к нулю и получим $$(x-1)^2 e^{x+1} => x-1=0 => x=1$$Получили точку пересечения с осью \(Ox\): (1;0).
3.2. Точки пересечения с осью \(Oy\). Это точки у которых \(x = 0\). Приравняем к нулю и получим $$(0-1)^2 e^{0+1} = e => y = e$$Получили точку пересечения с осью \(Oy\): (0;e).
4. Определим четность функции. \(f(-x)=(-x-1)^2 e^{-x+1}\) - функция не является ни четной, ни нечетной.
5. Найдем интервалы монотонности функции и критические точки (экстремумы и точек перегиба) .
Найдем критические точки и определим, какие из них являются экстремумами, точками перегибы. Для этого найдем первую производную и приравняем ее к 0.
$$y'=((x-1)^2 e^{x+1})' = 2(x-1)e^{x+1} + (x-1)^2e^{x+1} =$$$$= (x-1)e^{x+1}(2 + (x-1)) = (x-1)e^{x+1}(x+1) = 0 =>x_1 = 1, x_2 = -1 $$Получили две критические точки. Определим являются ли они экстремумами или точками перегиба. Для этого рассмотрим знак производной справа и слева от критических точек, т.е. знак производной на интервалах \((-\infty;-1) \cup (-1;1) \cup (1; +\infty)\)
\(x \in (-\infty;-1)\): \(f'(-2) = (x-1)e^{x+1}(x+1) = (-2-1)e^{-2+1}(-2+1) > 0\), т.е. функция возрастает
\(x \in (-1;1)\): \(f'(0) = (x-1)e^{x+1}(x+1) = (0-1)e^{0+1}(0+1) < 0\), т.е. функция убывает
\(x \in (1; +\infty)\): \(f'(2) = (x-1)e^{x+1}(x+1) = (2-1)e^{2+1}(2+1) > 0\), т.е. функция возрастает
Определили интервалы монотонности. Теперь можем сказать являются ли эти точки экстремумами или точками перегиба.
точка \(x = -1\), знак производной меняется с "+" на "-" -это точка локального максимума (экстремум), \(f(-1) = (x-1)^2 e^{x+1} = (-1-1)^2 e^{-1+1} = 4 =>\) координата точки локального максимума равна \((-1;4)\).
точка \(x = 1\), знак производной меняется с "-" на "+" -это точка локального минимума (экстремум), \(f(1) = (x-1)^2 e^{x+1} = (1-1)^2 e^{1+1} = 0 =>\) координата точки локального минимума равна \((1;0)\). Эта точка также является точкой пересечения с осью \(Ox\) (см. п3.1).
6. Найдем интервалы выпуклости. Как известно, выпуклость характеризует вторая производная, поэтому найдем ее, приравняем к 0, получим интервалы выпуклости и определим знак второй производной на этих интервалах. $$y'' = (y')' = ((x-1)e^{x+1}(x+1))' = ((x^2-1)e^{x+1})' = $$$$ =2xe^{x+1} + (x^2-1) = e^{x+1}(2x + x^2-1) = e^{x+1}(2x + x^2-1) = $$$$ =(x+1-\sqrt 2)(x+1+\sqrt 2)e^{x+1} = 0$$получили три интервала \((-\infty; -1-\sqrt 2) \cup (-1-\sqrt 2; -1+\sqrt 2) \cup (-1+\sqrt 2; +\infty)\). Определим знак второй производной на этих интервалах это даст нам информацию о выпуклости графиков функций на этих интервалах
\((-\infty; -1-\sqrt 2)\): \(f''(-3) = (x+1-\sqrt 2)(x+1+\sqrt 2)e^{x+1}= (-3+1-\sqrt 2)(-3+1+\sqrt 2)e^{-3+1} >0\) график функции имеет выпуклость вниз
\((-1-\sqrt 2; -1+\sqrt 2)\): \(f''(-1) = (x+1-\sqrt 2)(x+1+\sqrt 2)e^{x+1}= (-1+1-\sqrt 2)(-1+1+\sqrt 2)e^{-1+1} < 0\) график функции имеет выпуклость вверх
\(( -1+\sqrt 2; +\infty)\): \(f''(2) = (x+1-\sqrt 2)(x+1+\sqrt 2)e^{x+1}= (2+1-\sqrt 2)(2+1+\sqrt 2)e^{2+1} > 0\) график функции имеет выпуклость вниз
7. Исследуем поведение функции на границах области определения \(x \in (-\infty;+\infty)\), т.е. найдем пределы при \(x \to -\infty,x \to +\infty\) $$\lim_{x \to -\infty} (x-1)^2 e^{x+1} = \infty * e^{-\infty} = \infty * 0$$проведем некоторые преобразования, приведем к неопределенности вида \(\frac{0}{0}\) и найдем предел по правилу Лопиталя $$\lim_{x \to -\infty} (x-1)^2 e^{x+1} = \lim_{x \to -\infty} \frac{(x-1)^2}{\frac{1}{e^{x+1}}} = \frac{\infty}{\infty}$$применим правило Лопиталя $$\lim_{x \to -\infty} \frac{(x-1)^2}{\frac{1}{e^{x+1}}} = \lim_{x \to -\infty} \frac{2(x-1)}{-\frac{1}{e^{x+1}}} = \lim_{x \to -\infty} \frac{2}{\frac{1}{e^{x+1}}} = 0$$Пришлось дважды применять правило Лопиталя, находить производные числителя и знаменателя, т.к. после первого применения правило неопределенность \(\frac{\infty}{\infty}\) осталась.
Теперь найдем второй предел $$\lim_{x \to +\infty} (x-1)^2 e^{x+1} = + \infty$$
8. Построим график функции.