Решение:
для решения применим метод расстояний.
Найдем геометрической место точек, удовлетворяющих заданному условию.
Пусть точка с координатами A(x;y) удовлетворяет этим условиям:
1. расстояние от этой точки до прямой х= -3 равное \(d\)
2. расстояние \(d\) в два раза меньше расстояния до точки F(-12; 0), т.е равно \(2d\).
Расстояние от точки A(x;y) прямой х= -3 равно \(d = x-(-3) = x+3\)
Расстояние от точки A(x;y) до точки F(-12; 0) равно \(2d = \sqrt{(y-0)^2+(x+12)^2}\)
Приравняем эти расстояния
$$ 2(x+3)= \sqrt{(y-0)^2+(x+12)^2}=>$$$$4(x+3)^2 =y^2+(x+12)^2 =>$$
$$ 4x^2+24x+36 = y^2 + x^2+24x+144 =>$$$$ 3x^2 - y^2 =108 => $$$$ \frac{x^2}{6^2} - \frac{y^2}{(6\sqrt{3})^2} = 1$$
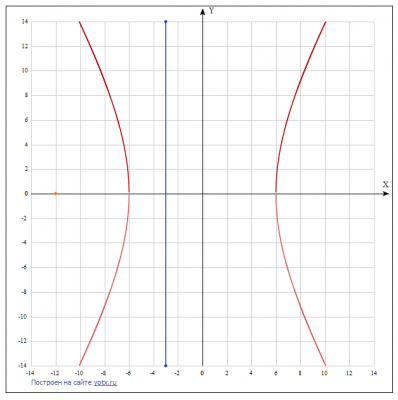
Ответ: получили уравнение гиперболы \(\frac{x^2}{6^2} - \frac{y^2}{(6\sqrt{3})^2} = 1\) с действительной осью симметрии Ox и мнимой осью симметрии Oy. Действительная полуось \(a = 6\), мнимая полуось \(b = 6\sqrt{3} \)
Построим график: