Cтавим уравнение касательной к кривой \(y=x^2- 6x+5\) в точках пересечения ее с осью абсцисс.
Уравнение касательной в точке имеет вод$$y = f(a) + f'(a)(x)$$где \(f(a)\) - значение функции в точке, \(f'(a)\) - угловой коэффициент касательной в точке, первая производная функции \(f(x)\) в точке. Общую теорию вспомнили, приступаем к решению.
1. Найдем точки касания \(a\). Согласно условия задачи - точки пересечения с осью \(Ox\). Точками пересечения с осью абсцисс являются корни уравнения $$x^2 - 6x + 5 = 0 => x_{1,2} = \frac{6 \pm \sqrt{36 - 4*5}}{2} = \frac{6 \pm 4}{2} => x_1 = 5, x_2 = 1$$Получили 2 точки касания, значение функции в этих точках равно 0, поэтому \(f(a) =0\)
2. Найдем первую производную в этих точках $$f'(x) = (x^2 - 6x + 5)' = 2x-6$$подставим значение точек касания $$f'(1) = 2x-6 = 2-6 = -4$$$$f'(5) = 2x-6 = 10-6 = 4$$
3. Мы получили две точки касания, т.е. понятно, что будет две касательные. Подставляем полученные данные, получим уравнение первой касательной в точке \(x = 1\)$$y = -4*(x-1) = -4x + 4 =>$$$$y = -4x + 4$$ уравнение второй касательной в точке \(x = 5\)$$y = 4 * (x - 5) = 4x - 20 =>$$$$y = 4x - 20$$
для проверки построим график заданной функции и касательные в точках к нему, которые мы получили.
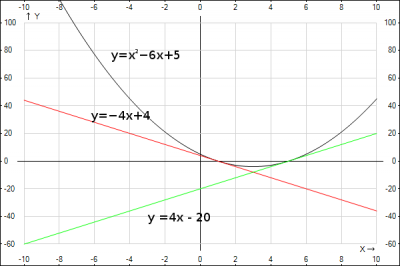
Ответ: уравнения касательных в точках пересечения с осью абсцисс графика функции \(y=x^2- 6x+5\) следующие \(y = -4x + 4\) и \( y =4x - 20\)





