Решение: разложим в ряд Фурье функцию $$ f(x) = \frac{1}{8} \pi(\pi-2x) $$
Определение: функция \(f(x)\) удовлетворяет условию Дирихле на отрезке [a;b], если она:
1. непрерывна на этом отрезке или имеет на этом отрезке конечное число точек разрыва первого рода;
2. кусочно-монотонная на отрезке [a;b], т.е. на этом отрезке может быть конечное число экстремумов.
Функция f(x) , которая задана на отрезке \([-\pi;\pi]\), удовлетворяет условию Дирихле, так как в каждой точке промежутка \([-\pi;\pi]\) она непрерывна и может быть записана в виде ряда Фурье $$f(x) = \frac{a_0}{2}+a_1\cos(x)+b_1\sin(x)+ ... + a_n\cos(nx)+b_n\sin(nx)+ ... = $$$$ = \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n\cos(nx)+b_n\sin(nx)) \quad (1)$$ называется тригонометрическим рядом.
Коэффициенты \(a_0,a_n,b_n\) ряда для \(2\pi\) периодической функции f(x) рассчитываются по формулам $$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx$$$$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx$$$$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dx$$ эти коэффициенты называются коэффициентами Фурье, а ряд $$\frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n\cos(nx)+b_n\sin(nx))$$ называется рядом Фурье.
Раскладываем в ряд Фурье функцию \(f(x) = \frac{1}{8} \pi(\pi-2x) \)
Найдем коэффициенты Фурье:
1. Коэффициент \( a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx\)
$$ a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi} \frac{1}{8} \pi(\pi-2x)dx = \frac{1}{8} \int_{-\pi}^{\pi} (\pi-2x)dx = $$$$ = \frac{1}{8} [ \pi*x - x^2|_{-\pi}^{\pi}] = \frac{1}{8} 2\pi^2 = \frac{1}{4}\pi^2$$
2. Коэффициент \( a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx \)
$$a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} \frac{1}{8} \pi(\pi-2x)\cos(nx)dx = $$$$ = \frac{1}{8}\int_{-\pi}^{\pi} (\pi-2x)\cos(nx)dx = \frac{\pi \sin(n\pi)}{4 n} = 0$$
3. Коэффициент \( b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dx \)
$$b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} \frac{1}{8} \pi(\pi-2x) \sin(nx)dx = $$$$ = \frac{1}{8} \int_{-\pi}^{\pi} (\pi-2x) \sin(nx)dx = \frac{4n\pi \cos(n\pi) -4\sin(n\pi)}{8n^2} = $$$$ = \frac{4n\pi \cos(n\pi) -0}{8n^2} = \frac{\pi \cos(n\pi)}{2n} = (-1)^n \frac{\pi}{2n}$$
Подставляем найденный коэффициенты в формулу ряда Фурье (1), получаем $$ f(x) = \frac{1}{8}\pi^2 + \sum_{n=1}^{\infty}(-1)^n \frac{\pi}{2n}\sin(nx) => $$$$ \frac{1}{8} \pi(\pi-2x) = \frac{1}{8}*\pi^2 - \frac{\pi}{2}*\sin(x)+ \frac{\pi}{4}*\sin(2x) +$$$$ + ... + (-1)^n \frac{\pi}{2n}\sin(nx)$$
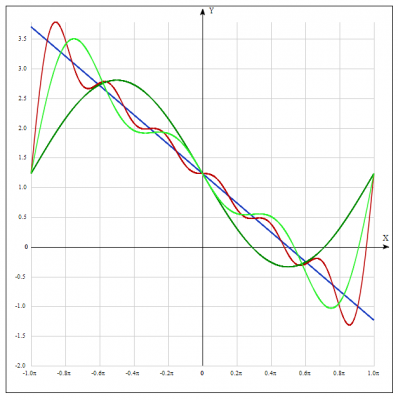
Строим график функции:
Из графика функции видно, что при увеличении количества членов ряда Фурье график суперпозиции периодических функций ряд приближается к графику функции \(f(x) = \frac{1}{8} \pi(\pi-2x)\), раскладываемую и ряд Фурье.