Три стрелка независимо друг от друга стреляют каждый по своей мишени один раз. Вероятности попадения

Построим ряд распределения случайной величины - попадание в мишень. Нам необходимо установить связь между значениями случайной величины (попадание в мишень) и соответствующими вероятностями.

Для начала запишем вероятности попадания и промаха для каждого из стрелков
для первого стрелка - $p_1=0,3$ - вероятность попадания в цель, $q_1= 1 - p_1 = 0,7$ -  вероятность промаха
для второго стрелка - $p_2=0,6$ - вероятность попадания в цель, $q_2= 1 - p_2 = 0,4$ -  вероятность промаха
для второго стрелка - $p_3=0,7$ - вероятность попадания в цель, $q_3= 1 - p_3 = 0,3$ -  вероятность промаха

Случайная величина может $X$ принимать следующие значения:
$x_0 = 0$ - никто из спортсменов не попал в мишень ,
$x_1 =1$ - попали в одну из мишеней,
$x_2=2$ -  попали в две мишени,
$x_3=3$ - попали в три мишени.
На основании полученных данных рассчитаем вероятности для каждой случайной величины и заполним таблицу - ряд распределения случайной величины
$x_0$ - никто из спортсменов не попал в мишень, т.е. находится совместное наступление событий - все спортсмены промахнулись $P_0 = q_1*q_2*q_3 = 0,7*0,4*0,3 =0,084$

$x_1$ - один из спортсменов попал в мишень, рассчитаем 3 вероятности - первый попал остальные промахнулись $p_1*q_2*q_3$ + второй попал, остальные нет $q_1*p_2*q_3$ + третий попал остальные нет $q_1*q_2*p_3$, получили $P_1 = p_1*q_2*q_3 + q_1*p_2*q_3 + q_1*q_2*p_3  = 0,3*0,4*0,3 + 0,7*0,6*0,3 + 0,7*0,4*0,7 = 0,358$

$x_2$ - два спортсмена попали в мишени, рассчитаем вероятность как и в предыдущем случае, только учтем, что в этот раз попали в 2 мишени $P_2 = p_1*p_2*q_3 + p_1*q_2*p_3 + q_1*p_2*p_3 = 0,3*0,6*0,3 + 0,3*0,4*0,7 + 0,7*0,6*0,7 = 0,432$

$x_3$ - все спортсмены попали в мишени $P_3 = p_1*p_2*p_3 = 0,3*0,6*0,7 = 0,126$ подставим полученные результаты в таблицу

$$\begin{array}{|c|c|} \hline \\ x_0 &  x_1 &  x_2 &  x_3  \\ \hline \\ q_1*q_2*q_3 = & p_1*q_2*q_3+ & p_1*p_2*q_3+ & p_1*p_2*p_3=  \\ & q_1*p_2*q_3+ & p_1*q_2*p_3+ &\\  & q_1*q_2*q_3 =& q_1*p_2*p_3 = &  \\ \hline \\ 0,084 & 0,358 & 0,432 & 0,126 \\ \hline \end{array}$$ Проверим правильность построения ряда распределения случайной величины: сумма вероятностей всех возможных значений случайной величины равна 1. Проверим это 0,084+0,358+0,432+0,126 = 1.Ряд распределения случайной величины построен правильно.

Найдем функцию распределения: функция распределения строится на основании ряда распределения с помощью выражения

$$F(x) = \sum_{x_i < x}P(X = x_i)$$ Сроим функцию распределения случайной величины.
1. При $x \leq 0$ $F(x) = \sum_{x_i < 0}P(X = x_i) = 0$
2. При $0 < x \leq 1$ $F(x) = \sum_{x_i < 1}P(X = x_i) = P(X = 0) = 0,084$
3. При $1 < x \leq 2$ $F(x) = \sum_{x_i < 2}P(X = x_i) = P(X = 0) + P(X = 1) = 0,084 + 0,358 = 0,442$
4. При $2 < x \leq 3$ $F(x) = \sum_{x_i < 3}P(X = x_i) = P(X = 0) + P(X = 1) + P(X = 2) = 0,084 + 0,358 + 0,432 = 0,874$
5. При $3 < x$ $F(x) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0,084 + 0,358 + 0,432 + 0,126 = 1$

 График функции распределения представлен на рис. 1

 

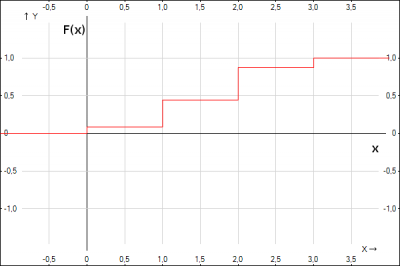
Найдем математическое ожидание  числа пораженных мишеней:
Математическим ожиданием $M[X]$ случайной величины $X$ называется сумма произведений всех возможных значений случайной величины на вероятность этих значений

$$M[X] = \sum_{i=1}^{\infty}x_ip_i$$ Найдем математическое ожидание $$M[X] = x_0*P_0 + x_1*P_1 + x_2*P_2 + x_3*P_3 = 0*0,084 + 1*0,358 + 2*0,432 + 3*0,126 = 1,6$$ Математическое ожидание равно $M[X]=1,6$ попадания в мишени.

Найдем среднее квадратичное отклонение числа пораженных мишеней:
Дисперсией случайной величины называется математическое ожидание квадрата отклонения величины от ее математического ожидания

$$D[X] =M[(X-m_x)^2]$$ для дискретной случайной величины дисперсия выражается суммой $$D[X] = \sum_{i=1}^n(x_i-m_x)^2P_i$$ Дисперсия - характеристика рассеивания возможных  значений случайной величины, но она имеет размерность квадрата случайной величины. Для большего удобства используют среднеквадратическое отклонение случайной величины $X$ той же размерности что и $X$ $$\sigma_x = \sqrt{D[X]} => \sigma_x = \sqrt{\sum_{i=1}^n(x_i-m_x)^2P_i}$$ подставляем полученные данные $$\sigma_x = \sqrt{(x_0 - m_x)^2P_0 + (x_1 - m_x)^2P_1 + (x_2 - m_x)^2P_2 + (x_3 - m_x)^2P_3}$$ $$\sigma_x = \sqrt{(0 - 1,6)^2*0,084 + (1 - 1,6)^20,358 + (2 - 1,6)^20,432 + (3 - 1,6)^20,126}$$ $$\sigma_x = \sqrt{1,6^2*0,084 + 0,6^20,358 + 0,4^20,432 + 1,4^20,126} \approx  0,81$$

Найти вероятность того,что пораженных мишеней будет:

Указанные вероятности можно искать по разному. У нас есть функция распределения. На основании ее свойства и будем находить:

Вероятность появления случайной величины в интервале $[\alpha;\beta)$, равна разности значений функции распределения в концах интервала, т.е.

$$P(\alpha \leq x <  \beta) = F(\alpha) - F(\beta)$$ Смотрим рис.1

а)хотя бы одна;

Это значит, что необходимо найти вероятность, что промаха не будет, т.е. интервал будет $([1;3) => P([1;3))  = P(3) - P(1) = 1 - 0,084 = 0.916$
или воспользуемся данными ряда распределения случайной величины $P = P_1+P_2+P_3 = 0,358 + 0,432 + 0,126 = 0,916$

б)менее двух.

Это значит, будет 0 или 1 попадание , т.е. интервал будет $[0;1) => P([0;1))  = P(1) - P(0) = 0,442 - 0 = 0,442$
или воспользуемся данными ряда распределения случайной величины $P = P_0+P_1 = 0,084 + 0,358  = 0,442$