Решение:
пусть граница области D задана параметрическими уравнениями \(x = x(t); \quad y =y(t)\), где \(t_1 \leq t \leq t_2\), где функции \(x(t); y(t)\) - непрерывно дифференцируемые на отрезке \([t_1;t_2]\). Если при движении вдоль границы от \(t_1\) к \(t_2\) область D остается слева, то ее площадь может быть рассчитана по формуле $$S = - \int_{t_1}^{t_2}x'(t)y(t)dt \quad (1)$$$$S = \int_{t_1}^{t_2}x(t)y'(t)dt \quad (2)$$$$S = \frac{1}{2}\int_{t_1}^{t_2}[x(t)y'(t) - x'(t)y(t)]dt \quad (3)$$
В задании представлено уравнение циклоиды. При движении точки вдоль первой арки циклоиды параметр \(t\) меняется от \(0\) до \(2\pi\), т.к. \(y(0) = y(2\pi)=0\) в других точках указанного промежутка \(y > 0 \).
При таком направлении обхода границы область находится справа, т.е. при использовании формулы изменим знак на противоположный (применим, например, формулу (1)) $$S = \int_{t_1}^{t_2}x'(t)y(t)dt$$
Найдем границы отрезка \([t_1;t_2]\).
Строим циклоиду
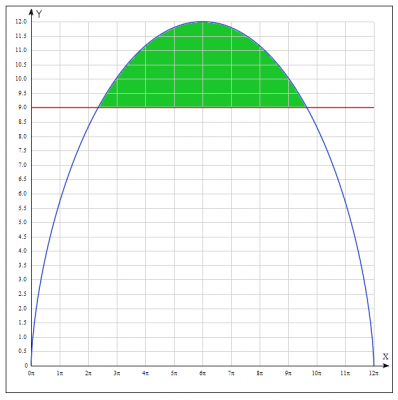
Согласно условия задачи \( 0 \leq x \leq 12\pi => 0 \leq 6(t- \sin(t)) \leq 12\pi => 0 \leq t \leq 2\pi\)
Подставим значения \(y \geq 9\), получаем $$ 6(1-\cos(t)) \geq 9 => -\frac{1}{2} \geq \cos(t) => \cos(t) \leq -\frac{1}{2} => $$ значение параметра \(t\) будем брать на отрезке \([0;2\pi]\) $$\begin{cases}0 \leq x \leq 2\pi\\ \frac{2}{3}\pi(3n+1) \leq t \leq \frac{2}{3}\pi(3n+2), n \in Z\end{cases} => $$$$ \begin{cases}0 \leq x \leq 2\pi\\ \frac{2}{3}\pi \leq t \leq \frac{4}{3}\pi, n=0 \end{cases} $$ Подставляем границы $$S = \int_{\frac{2}{3}\pi }^{{\frac{4}{3}\pi }}(6(t- \sin(t))'6(1-\cos(t))dt = 36\int_{\frac{2}{3}\pi }^{{\frac{4}{3}\pi }}(1- \cos(t))^2dt = $$$$ =36\int_{\frac{2}{3}\pi }^{{\frac{4}{3}\pi }}(1- 2\cos(t) + \cos(t)^2)dt = $$ применяем формулу косинуса двойного угла \( \cos^2(x) = \frac{1 + \cos(2x)}{2}\) $$ = 36\int_{\frac{2}{3}\pi }^{{\frac{4}{3}\pi }}(1- 2\cos(t) + \frac{1+\cos(2t)}{2})dt =$$$$ = 36\int_{\frac{2}{3}\pi }^{{\frac{4}{3}\pi }}( \frac{3}{2}- 2\cos(t) + \frac{\cos(2t)}{2})dt =$$$$ = 36( \frac{3}{2}t - 2\sin(t) + \frac{ \sin(2t)}{4})|_{\frac{2}{3}\pi }^{{\frac{4}{3}\pi }} = 9(9\sqrt{3}+4\pi) \approx 253.39 $$
Ответ: площадь фигуры, ограниченной линиями, заданными параметрическими уравнениями равна \(S \approx 253.39 \)



