Рішення: знайдемо площу фігури, обмежену лініями \(y = x^2 + 5x + 2; \quad -2x + y-6 = 0 \)
Будуємо криві:
1. \( y = x^2 + 5x + 2 \) - парабола.
Проведемо перетворення рівняння, виділимо повний квадрат $$ x^2 + 5x + 2 = x^2 + 2*\frac{5}{2}x + \frac{25}{4} - \frac{25}{4}+2 = $$$$ = (x + \frac{5}{2})^2 - \frac{25}{4}+2 => y = (x + \frac{5}{2})^2 - \frac{17}{4} $$ Отримали рівняння параболи з центром в точці \((- \frac{ 5}{2}; - \frac{17}{4}) \), осі якої спрямовані вгору.
2. \( -2x + y-6 = 0 => y = 2x + 6 \) - рівняння прямої.
Будуємо малюнок:
Потрібно знайти площу криволінійної фігури \(ABC \)
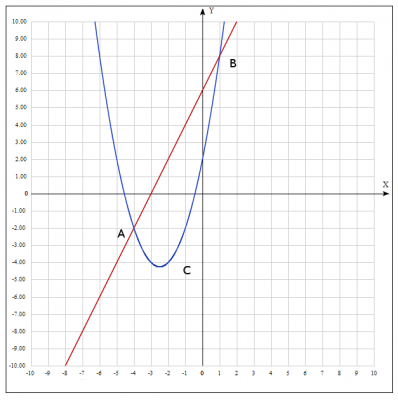
Згадаймо геометричний зміст визначеного інтеграла: якщо фігура обмежена кривими \(y_1 = g (x) \) і \(y_2 = f (x) \), причому функція \(f(x) > g(x) \),
то визначений інтеграл \(S = \int_a^b [f(x) - g(x)]dx \) дорівнює площі цієї фігури.
Згідно умови задачі \( y_2 = 2x + 6; \quad y_2 = x^2 + 5x + 2 \), тоді шукана площа фігури \(ABC \) дорівнює $$ S_{ABC} = \int_a^b (2x + 6 - (x^2 + 5x + 2)) dx =
\int_a^b (4 - x^2 - 3x)dx $$ для знаходження інтеграла потрібно знайти координати \(x \) точок \(a\) і \(b\). Це точки перетину кривих, тому вирішимо систему рівнянь $$ \begin{cases} y = 2x + 6 \\ y = x^2+ 5x + 2 \end{cases} => \begin{cases} y_1 = -2; y_2 = 8 \\ x_1 = -4; x_2 = 1 \end{cases} $$ Підставляємо координати \(x \) точок в інтеграл $$ S_{ABC} = \int _{- 4}^{1} (4-x ^ 2-3x) dx = $$ Для знаходження визначеного інтеграла, застосуємо формулу Ньютона-Лейбніца \( \int_a^bf(x)dx = F (x) |_a ^ b = F (b) - F (a) \), отримуємо $$ = 4x - \frac{x ^ 2}{3} - \frac{3}{2} x^2 |_{- 4}^{1} = \frac{125}{6} = \approx 20.83 $$
Відповідь: площа фігури, яка обмежена лініями \(y = x^2 + 5x + 2 \quad -2x + y-6 = 0 \) дорівнює \(S_{ABC} = \frac{125}{6} = \approx 20.83 \)
2. Обчислити об'єм тіла, отриманого обертанням фігури навколо осі Oy, яка обмежена лініями, \(x = 0; \quad x > 0; \ quad y = x^2 + 5x + 2; \ quad -2x + y-6 = 0 \).
Якщо тіло отримано шляхом обертання криволінійної трапеції, обмеженої кривими \(y_1 = f (x); y_2 = g (x) \) (при цьому \(0 \leq f(x) \leq g(x) \)) і прямими \(x = a \) і \(x = b \) навколо осі \(Oy \), обсяг розраховується за формулою $$ V_y = 2 \pi \int_a^bx (y_2-y_1) dx \quad (1) $$
У завданні фігура обмежена кривими $$ y_2 = 2x + 6; y_1 = x^2 + 5x + 2 $$
Межі
\(a \) -> \(x = 0 \)
\(b \) -> точка перетину кривих, була знайдена в п.1 \(x = 1 \)
Підставляємо дані у формулу (1), отримуємо $$ V_y = 2 \pi \int_0^1x (2x + 6 - x^2 - 5x - 2) dx = 2 \pi \int_0^1x ( 4 - x^2 - 3x) dx = $$ застосуємо формулу Ньютона-Лейбніца \( \int_a^bf(x)dx = F(x) |_a^b = F(b) - F( a) \), отримаємо $$ = 2 \pi [2x^2 - \frac {x^4}{4} - x^3] |_0^1 = \frac{3}{2} \pi $$
Відповідь : об'єм тіла, отриманого обертанням фігури навколо осі Oy, яка обмежена лініями \(x = 0; \quad x > 0; \quad y = x^2 + 5x + 2; \quad -2x + y-6 = 0 \) дорівнює \( V_y = \frac{3}{2} \pi \)



