Для нахождения вероятности рассмотрим рисунок.
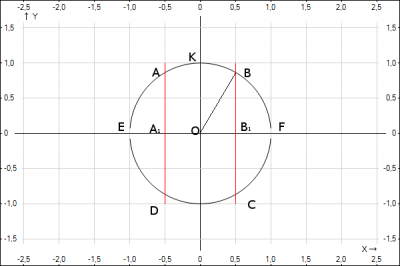
По определению геометрической вероятности искомая вероятность равна отношению площадей $$P = \frac{S_{ABCD}}{S_{kr}} = \frac{S_{ABCD}}{\pi r^2}$$Необходимо найти \(S_{ABCD}\). Из рисунка видно, что \(S_{ABCD} = 4S_{OKBB_1}\). Найдем площадь фигуры $$S_{OKBB_1} = S_{KOF} - S_{BB_1F} => S_{ABCD} = 4S_{KOF} - 4S_{BB_1F} = S_{kp} - 4S_{BB_1F}$$
\(S_{BB_1F}\) - площадь , которую можно представить как \(S_{BB_1F} = S_{BOF} - S_{ΔBOB_1}\). Найдем площадь сектора \(S_{BOF} = S_{kp}*\frac{ \underline{/}BOF}{360^0}\). Угол \(\underline{/}BOF\) найдем из треугольника прямоугольного \(ΔBOB_1\). Катет \(OB_1\) по условию в 2 раза меньше гипотенуза, значит угол \(\underline{/} OBB_1 = 30^0 => \underline{/} BOF = 90^0-30^0 = 60^0\). Подставим в площадь сектора и получим $$S_{BOF} = S_{kp}*\frac{\underline{/}BOF}{360^0} = \pi r^2 * \frac{60^0}{360^0} = \pi r^2 * \frac{1}{6} => $$$$S_{BB_1F} = S_{BOF} - S_{ΔBOB_1} => $$$$S_{BB_1F} = \frac{1}{6} \pi r^2 - \frac{1}{2}*OB_1*BB_1 = \frac{1}{6} \pi r^2 - \frac{1}{2}*\frac{r}{2} r* \sin 60^0 = \frac{1}{6} \pi r^2 - \frac{1}{4}* r^2*\frac{\sqrt 3}{2} $$ Подставим результаты в формулу площади \(S_{ABCD}\) и получим $$S_{ABCD} = S_{okp} - 4S_{BB_1F} = \pi r^2 - 4( \frac{1}{6} \pi r^2 - \frac{1}{4}* r^2*\frac{\sqrt 3}{2}) =$$$$= \pi r^2 - 4\frac{1}{6} \pi r^2 + 4\frac{1}{4}* r^2*\frac{\sqrt 3}{2} = \frac{1}{3} \pi r^2 + r^2*\frac{\sqrt 3}{2} $$А теперь подставим результата в формулу вероятности $$P = \frac{S_{ABCD}}{S_{kr}} = \frac{\frac{1}{3} \pi r^2 + r^2*\frac{\sqrt 3}{2}}{\pi r^2} =>$$учтем, что окружность единичная, т.е. \(r = 1\) $$P = \frac{1}{3} + \frac{\sqrt 3}{2\pi} \approx 0,61$$
Получим этот же результат другим методом. Вспомним, что площадь фигуры можно найти используя определенный интеграл. Вспомним уравнение окружности с центром в начале координат \(x^2+y^2 = r^2 = > y = \pm \sqrt {r^2 - x^2}\). Т.к. мы рассматриваем площадь фигуры в первой четверти и \(r = 1\), получим $$S_{OKBB_1}= \int_0^{\frac{1}{2}}\sqrt{1-x^2}dx = $$Для нахождения интеграла воспользуемся основной формулой интегрального исчисления $$\int_a^b f(x) dx = \Phi(x)|_a^b \quad (1)$$ Найдем интеграл $$\int \sqrt{1-x^2}dx = $$ избавимся от иррациональности путем введения замены \(x = \sin t => dx = \cos t dt\) получим $$ = \int \sqrt{1-\sin^2 t}\cos tdt = \int \sqrt{\cos^2 t}\cos tdt = \int \cos^2 t dt =$$применим формулу косинуса двойного угла \(\cos 2x = 2\cos^2 x - 1 => \cos^2 x = \frac{\cos 2x +1}{2}\) $$\int \frac{\cos 2t +1}{2} dt = \frac{1}{2}\int \cos 2t dt + \frac{1}{2} \int dt = $$для первого интеграла применим замену переменной \(2t = u => dt = \frac{1}{2}du\) $$=\frac{1}{2}\int \frac{1}{2}\cos u du + \frac{1}{2} t = \frac{1}{4} \sin u + \frac{1}{2} t =$$проведем обратную замену \(u = 2t\)$$\frac{1}{4} \sin 2t + \frac{1}{2} t =$$применим формулу синуса двойного угла \(\sin 2x = 2\sin x*\cos x\)$$\frac{1}{4} 2\sin t*\cos t + \frac{1}{2} t = \frac{1}{2} \sin t*\sqrt{1-\sin^2 t} + \frac{1}{2} t =$$проведем обратную замену \(x = \sin t => t = \arcsin x\)$$ =\frac{1}{2} x \sqrt{1-x^2 } + \frac{1}{2} \arcsin x +C$$подставим полученный результат в \(1\), получим $$\int_0^{\frac{1}{2}}\sqrt{1-x^2}dx = \frac{1}{2} x \sqrt{1-x^2 } + \frac{1}{2} \arcsin x |_0^{\frac{1}{2}} =$$$$ = \frac{1}{2} \frac{1}{2} \sqrt{1-(\frac{1}{2})^2 } + \frac{1}{2} \arcsin \frac{1}{2} = \frac{\sqrt 3}{8} + \frac{1}{2} \frac{\pi}{6} $$отсюда находим вероятность при \(r = 1\) $$P = \frac{4*S_{OKBB_1}}{\pi} = \frac{4*\frac{\sqrt 3}{8} + \frac{1}{2} \frac{\pi}{6}}{\pi} => $$$$P = \frac{\sqrt 3}{2\pi} + \frac{1}{3} \approx 0,61$$Решая задачу разными методами мы получили одинаковый результат.
Ответ: вероятность равна \(P \approx 0, 61 \)



