Решение: Дано уравнение кривой второго порядка \( 3x^2 +6x-3y+5=0 \)
Запишем уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
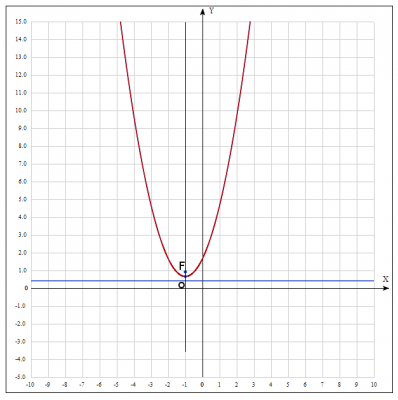
$$ 3x^2 +6x-3y+5=0 => x^2 +2x-y+\frac{5}{3}=0 =>$$ дополняем члены \(x^2+2x\) до полного квадрата \(x^2+2x+1\)$$ x^2 +2x + 1-1 -y+\frac{5}{3}=0 => (x+ 1)^2 -y+\frac{2}{3}=0 => $$$$ y - \frac{2}{3}= (x+ 1)^2 $$ Получили уравнение параболы. Приведем его к каноническому виду, сделаем замену координат \(y' = y - \frac{2}{3}; \quad x' = x+1\), получаем каноническое уравнение параболы $$y' = x'^2$$ вершина параболы имеет координаты \(O(-1; \frac{2}{3})\), а ось симметрии это прямая \(x = -1\). Каноническое уравнение параболы имеет вид \(x^2 = 2py\), т.е. получаема, что параметры равен \(2p=1 => p=\frac{1}{2}\)
Фокусом параболы является точка, которая лежит на оси симметрии на расстоянии \(\frac{p}{2} = \frac{1}{4}\) от вершины, т.е. координаты фокуса \( F(-1;\frac{2}{3}+\frac{1}{4}) => F(-1;\frac{11}{12}) \).
Уравнение директрисы в системе координат x'Oy' имеет вид \(y'=-\frac{p}{2} = -\frac{1}{4}\), тогда в системе координат xOy получаем \(y' = y - \frac{2}{3} => -\frac{1}{4} = y - \frac{2}{3} => y = \frac{5}{12} \)