Дано: \(q = 50 нКл = 50 * 10^{-9} Кл\), \(m = 0,2 г = 2*10^{-4} кг\), \(E = 8 кН/Кл = 8*10^3 Н/Кл\)
Найти: \(\alpha\)
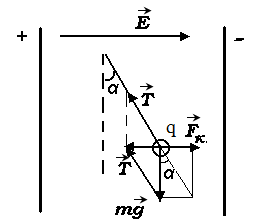
Решение: из рисунка видно, что равновесный угол отклонения \(\alpha\) определяется из условия \(\mbox{tg}\alpha = \frac{F}{P}\), где \(F = |q|E\) - электрическая сила, \(P=mg\) - сила тяжести; тогда $$\mbox{tg}\alpha = \frac{F}{P} = \frac{|q|E}{mg} = \frac{50*10^{-9}*8*10^3}{2*10^{-4}*9,8} = 0,204$$откуда $$\alpha = \mbox{arctg(0,204)} = 11,5^0$$Ответ: нить образует с вертикалью угол равный \(\alpha = 11,5^0\)

