Решаем уравнение $$ \cos(\frac{\pi}{2}-2x)=\sqrt 2 \cos x => $$ данное уравнение на знание формулы синуса двойного угла \(\sin 2x = 2\sin x*\cos x\), а для начала применим формулу приведения \( \cos (\frac{\pi}{2} -x) = \sin x\), получим $$ \sin(2x)=\sqrt 2 \cos x => 2\sin x *\cos x -\sqrt 2 \cos x = 0 =>$$$$2\cos x (\sin x -\frac{\sqrt 2}{2}) = 0 => \left[ \begin{gathered} \cos x = 0\\ \sin x -\frac{\sqrt 2}{2} =0 \end{gathered}\right. => $$$$\left[ \begin{gathered} \cos x = 0\\ \sin x = \frac{\sqrt 2}{2} \end{gathered}\right. => \left[ \begin{gathered} x = \pi n, n \in Z \\ \ x = (-1)^n*\frac{\pi}{4} + \pi n , n \in Z \end{gathered}\right. $$
По условию задачи необходимо найти корни уравнения на промежутке \([-6\pi;-5\pi]\). Для первого уравнения видно, что корни при \(n = -5, n=-6\) попадают в нужный промежуток \(x = -6\pi; x =-5\pi\), для второго уравнения рассмотрим рисунок
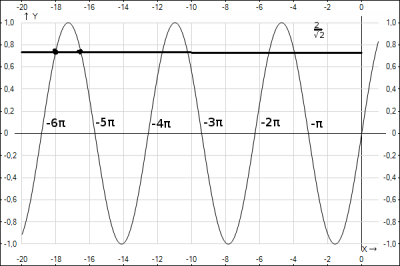
из рисунка видно, что корни уравнения \(\sin x = \frac{\sqrt 2}{2}\) попадают в нужный отрезок также при \(n = -5; n=-6\), получим \(n = -5; x = (-1)^n*\frac{\pi}{4} + \pi n => x = (-1)^{-5}*\frac{\pi}{4} - 5\pi => x = -\frac{\pi}{4} - 5 \pi => x = -5 \frac{1}{4}\pi\),
при \(n=-6\), получим \(x = (-1)^n*\frac{\pi}{4} + \pi n => x = (-1)^{-6}*\frac{\pi}{4} - 6\pi => x = \frac{\pi}{4} - 6\pi => x = -5 \frac{3}{4}\pi\)
Ответ: корни уравнения на промежутке \([-6\pi;-5\pi]\) следующие : \( -6\pi; -5\pi;-5 \frac{1}{4}\pi;-5 \frac{3}{4}\pi \)



