Решим уравнение $$\sin x+\sin^2\frac{x}{2} = \cos^2\frac{x}{2} =>$$ данное уравнение на знание формулы косинуса двойного угла \( \cos {2x} = \cos^2 x - \sin^2 x \), подставим формулу в уравнение и получим $$\sin x = \cos^2\frac{x}{2} -\sin^2\frac{x}{2} => \sin x = \cos x => $$$$\sin x - \cos x =0 => \cos x * (\mbox{tg}x -1) =0 =>$$\( \cos x \ne 0\), т.к. при \( \cos x =0 => \sin x = 1\), а по условию разность синуса и косинуса равна 0$$ \mbox{tg}x -1=0 => \mbox{tg}x =1 =>$$$$ x = \frac{1}{4}\pi + \pi n, n \in Z$$Ответ: \(x \in \frac{1}{4}\pi + \pi n, n \in Z\)
Найдем корни удовлетворяющие отрезку \([-2\pi;-\frac{\pi}{2}]\).
рассмотрим единичную окружность
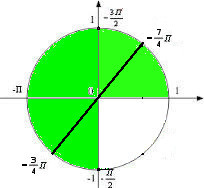
зеленым обозначен заданный отрезок, выбираем углы из ответа, удовлетворяющие заданному отрезку, это будут \(\frac{1}{4}\pi - \pi = -\frac{3}{4}\pi \) и \(\frac{1}{4}\pi - 2\pi = -\frac{7}{4}\pi \).
Ответ: корни, удовлетворяющие заданному отрезку равны \(-\frac{3}{4}\pi ; -\frac{7}{4}\pi\)



