Решение:
а) дифференциальную функцию f(x) (плотность распределения вероятности)
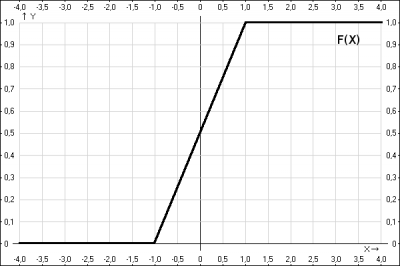
В точках дифференцируемости функции распределения \(F(x)\) ее производная равна плотности распределения \(f(x) = F(x)\)
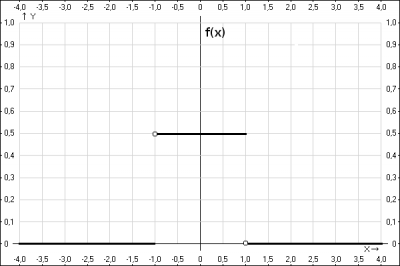
$$f(x) = (0)' = 0;\quad f(x) = (\frac{x+1}{2})' = \frac{1}{2}; \quad f(x) = (1)' = 0$$ получили плотность распределения $$f(x) \begin{cases}0, \text{при x} \leq-1\\\frac{1}{2}, \text{при -1} < x\leq1\\0, \text{ при x} > 1\end{cases}$$
б) вероятность попадания случайной величины в интервал (0;3)
Вероятность попадания значений случайной величины \(X\) в интервале (a;b) равна определенному интегралу по плотности распределения \(f(x)\) по отрезку [a;b], т.е. \( P(a < X < b) = \int_a^b f(x)dx \)
Применяем формулу $$P(0 < X < 3) = \int_0^3 f(x)dx = \int_0^1 \frac{x+1}{2}dx + \int_1^3 0dx = \frac{1}{2}(\frac{1}{2}x^2+x)|_0^1 = \frac{1}{2}(\frac{1}{2}1^2+1) = \frac{3}{4}$$
Ответ: вероятность попадания случайной величины в интервал (0,3) равна \(P(0 < X < 3) = \frac{3}{4}\)
в) математическое ожидание и дисперсию
Математическое ожидание
Математическое ожидание непрерывной случайной величины X, все значения которой принадлежат отрезку [a;b], а \(f(x)\) - ее плотность распределения вероятностей, определяется формулой \(M(X) = \int_a^b xf(x)dx\)
Найдем математической ожидание $$M(X) = \int_{-\infty}^{\infty} xf(x)dx = \int_{-\infty}^{-1} x*0dx + \int_{-1}^1 x \frac{1}{2}dx + \int_{1}^{\infty} x 0dx = \frac{1}{4}x^2|_{-1}^1 = 0$$
Ответ: математической ожидание равно \(M(X) = 0\)
Дисперсия
Дисперсией, или рассеиванием, случайной величины \(X\) называется математическое ожидание квадрата ее отклонения \(D(X) = M(X-M(x))^2\), для расчета используется формула \(D(X) = M(X^2)-(M(X))^2\)
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку [a;b], определяется формулой \(D(X) = \int_a^b(x-M(X))^2f(x)dx\), для расчета используется формула \(D(X) = \int_a^bx^2f(x)dx -M(X)^2\)
Находим дисперсию $$D(X) = \int_{-\infty}^{\infty}x^2f(x)dx -M(X)^2 = \int_{-1}^1x^2\frac{1}{2}dx -0 = $$$$ = \frac{1}{2}\frac{1}{3}x^3|_{-1}^1 = \frac{1}{6} + \frac{1}{6} = \frac{1}{3}$$
Ответ: дисперсия равна \(D(X) = \frac{1}{3}\)
г) построить графики F(x),f(x)