Составим уравнение касательной к кривой \(y=-x^2+2x-2\) параллельной оси абсцисс. Как известно у прямой параллельной оси абсцисс угловой коэффициент \(k=0\). Согласно геометрического смысла первой производной \(f'(a) = k\), т.е. первая производная в точке касания является угловым коэффициентом касательной. Т.е. в задаче необходимо найти точки у которых первая производная равна 0, а это есть экстремумы.
Ищем экстремумы $$y'=(-x^2+2x-2) = -2x+2$$приравняем производную к 0 $$ -2x+2 =0 =>x=1$$мы нашли экстремум. Найдем значение \(y\). \(f(1) = -x^2+2x-2 = -1+2-3 = -1\). Кривая \(y=-x^2+2x-2\) - парабола оси которой направлены вниз, а экстремум - вершина параболы имеет координату \((1;-1)\). Запишем уравнение кривой, параллельной оси абсцисс $$y = -1$$Сделаем чертеж
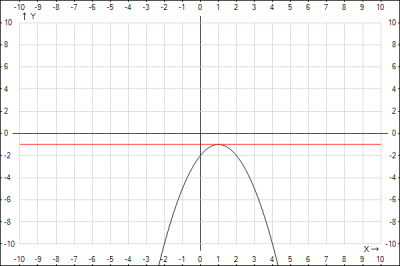
Ответ: уравнение касательной к кривой \(y=-x^2+2x-2\) параллельной оси абсцисс - \(y = -1\)



