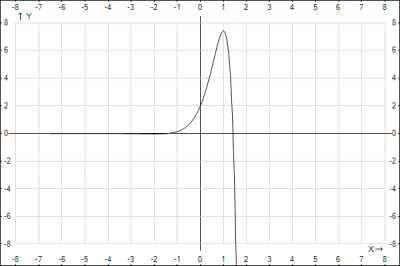
Исследуем функцию \(y=(2-x^2)e^{2x}\) и построить график. Для этого будем использовать общую схему исследования функции и построение графика
1. Найти область определения \(D_f\) и область значения \(E_f\) функции. Область определения и область значения вся числовая ось \(R\)
2. Изучим симметрию графика, выясним четность функция: \(f(-x)=(2-(-x)^2)e^{2(-x)} = (2-x^2)e^{-2x}\) - функция не является ни четной ни нечетной, т.е. она не является симметричной.
3. Найдем промежутки монотонности (возрастания и убывания). Для этого найдем первую производную, найдем критические точки (если они есть), т.е. приравняем производную к 0. На интервалах между критическими точками изучим монотонность функции, т.е. если производная больше 0 , то функция возрастает, если меньше 0, функция убывает. Находим производную $$y'=((2-x^2)e^{2x}) =$$применим формулу производной произведения и производной сложной функции$$= (2-x^2)'*e^{2x}+(2-x^2)(e^{2x})' = -2x*e^{2x}+(2-x^2)*e^{2x}*2 =$$$$= -2x*e^{2x}+4*e^{2x}-2x^2*e^{2x} = e^{2x}(-2x+4-2x^2)$$приравняем производную к 0, учтем , что \(e^{2x} >0\) по определению $$e^{2x}(-2x+4-2x^2) = 0 =>-2x+4-2x^2 = 0 =>x^2+x-2 =0 => $$$$x_{1,2} = \frac{-1 \pm \sqrt{1+4*2}}{2}=\frac{-1 \pm 3}{2} => x_1=1; x_2=-2$$Получили 2 критические точки. Найдем значения функции в этих точках \(f(-2) = (2-x^2)e^{2x} = (2-4)e^{-4} = -2e^{-4} \approx -0.036\) \(f(1) = (2-x^2)e^{2x} = (2-1)e^{2} = e^{2} \approx 7,39\)
Изучим знак производной слева и справа от критической точки
\(x = -2\) проверяем для точки слева \(f'(-3) =e^{2x}(-2x+4-2x^2) = e^{-6}(-2*(-3)+4-2*(-3)^2) < 0 \), т.е. на интервале \((-\infty;-2)\) функция убывает
\(x = -2\) проверяем для точки справа \(f'(0) =e^{2x}(-2x+4-2x^2) = e^{0}(-2*0+4-2*0) >0 \), т.е. на интервале \((-2;1)\) функция возрастает
Вывод: так как при переходе через критическую точку \(x=-2\) производная меняет знак с "-" на "+" эта точка с координатами (-2; -0.036) является экстремумом, точкой минимума.
\(x = 1\) проверяем для точки слева \(f'(0) =e^{2x}(-2x+4-2x^2) = e^{0}(-2*0+4-2*0) > 0 \), т.е. на интервале \((-2;1)\) функция возрастает
\(x = 1\) проверяем для точки справа \( f'(2) =e^{2x}(-2x+4-2x^2) = e^{4}(-2*2+4-2*2^2) < 0 \), т.е. на интервале \((1; +\infty)\) функция убывает
Вывод: так как при переходе через критическую точку \(x=1\) производная меняет знак с "+" на "-" эта точка с координатами (1; 7,39) является экстремумом, точкой максимума.
4. Найдем точки пересечения с осями:
с осью \(Ox\): при пересечении с осью \(Ox\) \(y=0\). Найдем точки \((2-x^2)e^{2x} = 0 =>2-x^2 =0 =>x = \pm \sqrt{2}\). Получили две точки пересечения с осью \(Ox\)
с осью \(Oy\): при пересечении с осью \(Oy\) \(x=0\). Найдем точки \(y = (2-x^2)e^{2x} =>y = (2-0^2)e^{2*0} => y = 2\). Получили одну точки пересечения с осью \(Oy\)
5. Рассмотрим поведение функции при \(x \to -\infty\) и \(x \to \infty\) $$\lim_{x \to -\infty}(2-x^2)e^{2x} = 0_{-}$$т.е при \(x \to -\infty\) \(y \to 0\) снизу.$$\lim_{x \to +\infty}(2-x^2)e^{2x} = -\infty$$ т.е. при \(x \to \infty\) \(y \to -\infty\)
6. Построим график, путем нанесения на него полученных результатов