Ищем наименьшее и наибольшее значения функции \( y= \sqrt{100-х^2} \) на отрезке \( [0;3] \).
Наибольшим, наименьшим значением функции на отрезке могут быть точки минимума, максимума или значения функции на концах отрезка.
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:
1. Находим стационарные точки:
Для нахождения стационарных точек найдем первую производную и приравняем ее у нулю $$y' = (\sqrt{100-х^2})' = -\frac{1}{2\sqrt{100-x^2}}*2x = -\frac{x}{\sqrt{100-x^2}}$$ приравняем производную к нулю $$ y' = -\frac{x}{\sqrt{100-x^2}} = 0 => x = 0$$ функция имеет одну стационарную точку \(x=0\), которая совпала с левой границей отрезка.
2 Выбираем из полученных стационарных точек те, которые принадлежат заданному отрезку.
Функция \(y\) отрезке [0;3] имеет точку вероятного экстремума (минимума, максимума) \(x = 0\).
3. Находим значения функции в выбранной стационарной точке (см п.2).
Найдем значение функции в этой точке $$f(0)= \sqrt{100-х^2} = 10$$
4. Находим значения функции на концах заданного отрезка:
$$f(3)= \sqrt{100-х^2} = \sqrt{91} \approx 9.5$$
5. Из полученных значений функции (п.3 и п.4) выбираем наибольшее и наименьшее значения.
Сравниваем результаты, полученные в п.3 и п.4
Наибольшим значением может быть точка максимума (если есть), если нет точки максимума, то сравниваем значения функции на концах отрезка.
Наименьшим значением может быть точка минимума (если есть), если нет точки минимума, то сравниваем значения функции на концах отрезка.
Наибольшее значение функции на отрезке - значение функции в левой границе (также является стационарной точкой) отрезка \(f(0) = 10 \), которая является точкой максимума.
Наименьшее значение функции на отрезке - значение функции в правой границе отрезка \(f(3) \approx 9.5 \)
Проверяем утверждение, что точка \(x = 0\) является точкой максимума, определяем знак первой производной слева и справа от стационарной точки.
\(f'(-1) = -\frac{x}{\sqrt{100-x^2}} > 0 \),
\(f'(1) = -\frac{x}{\sqrt{100-x^2}} < 0 \)
получили, что производная изменила знак с \( + \quad 0 \quad - \), т.е. это действительно точка максимума.
Т.о. в данном типе задач необязательно выяснять, является ли стационарная точка точкой экстремума, достаточно найти значение функции в этой точке и сравнить со значениями функции на концах отрезка.
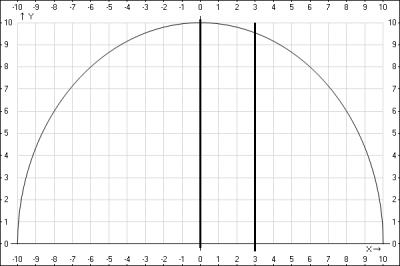
Проверяем полученный результат, строим график функции: