Знайти область визначення функції z=z(x,y) Побудувати область $$z=\frac{1}{\sqrt{x}}+\ln(x+2y-1)$$

Рішення: областю визначення функції $z = f(x;y)$ називається множина точок (x;y) площини xOy, у яких задана функція набуває певного дійсного значення.
Задана функція визначена, якщо підкореневий вираз $\sqrt{x}$ невід'ємний $x \geq 0$ та $x \ne 0$  тобто $x > 0$, також логарифмічна функція $\ln(x+2y-1)$ визначена, якщо аргумент логарифма задовольняє нерівність $x+2y-1 >  0$, таким чином для функції  $z=\frac{1}{\sqrt{x}}+\ln(x+2y-1)$ область визначення знаходимо із системи:
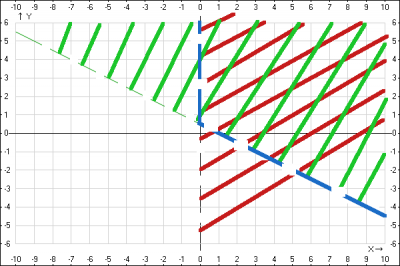
$$\begin{cases}x > 0 \\x+2y-1 >  0\end{cases} => \begin{cases}x > 0 \\ y > \frac{1}{2} - \frac{1}{2}x\end{cases}$$  
$x > 0$ - півплощина, розміщена праворуч осі Oy
$y > \frac{1}{2} - \frac{1}{2}x$ - півплощина, розміщена вище прямої $y = \frac{1}{2} - \frac{1}{2}x$