составить уравнения сторон треугольника, если дана одна его вершина В(-2;7), а также уравнения высот

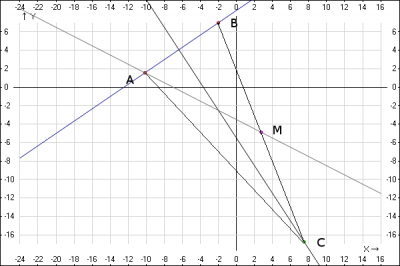
Решение: рассмотрим рисунок. Пусть высота выходит из вершины $C$, а медиана из вершина $A$.
1. Найдем уравнение стороны треугольника $AB$, на которую опущена высота треугольника $3x+2y+11=0 => y = -\frac{3}{2}x - \frac{11}{2}$.
Для уравнения искомой прямой известно координаты одной точки B(-2;7) и  угловой коэффициент, который найдем, воспользовавшись свойством угловых коэффициентов двух перпендикулярных прямых $k_1 = -\frac{1}{k_2}$, т.е. угловой коэффициент $k_{AB} = -\frac{1}{-\frac{3}{2}} = \frac{2}{3}$. Уравнение прямой AB найдем по формуле уравнения прямой, проходящей через заданную точку с известным угловым коэффициентом $y - y_0 = k(x-x_0)$, где $(x_0;y_0)$ - координаты известной точки, а $k$ - угловой коэффициент прямой, получаем

 2. Найдем координаты вершины  $A$.
Для этой вершины известно, что она является пересечением стороны $AB$ и медианы $x+2y+7=0$. Координаты вершины будем искать, составив систему уравнений

3. Найдем уравнение вершины $C$.
Пусть вершина имеет координаты $C(x_c;y_c)$. Пусть точка $M$ - точка пересечения медианы и стороны $BC$, тогда ее координаты будут рассчитываться по формуле $(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2})$, подставляем координаты точек $M(\frac{-2+x_C}{2}; \frac{7+y_C}{2})$, через данную точку проходит медиана $x_M+2y_M+7=0 => (\frac{-2+x_C}{2})+2\frac{7+y_C}{2}+7=0 => x_C +2y_C+26=0$. Известно что из вершины C выходит высота, т.е. истинно равенство $3x_C+2y_C+11=0$. Составим систему уравнений и найдем неизвестные $x_C,y_C$

4. Уравнения сторон треугольника.
Составим уравнения сторон $BC$ , $AC$. Для этих сторон известны координаты вершин треугольника, т.е. применим формулу уравнения прямой, проходящей через две заданные точки $\frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$
Подставляем координаты вершин 
$A(-\frac{71}{7}; \frac{11}{7})$, $C( \frac{15}{2};-\frac{67}{4})$ 
уравнение стороны AC

спасибо огромное