Найти промежутки возрастания и убывания функции и точки экстремума \(f(x)= e^x \sin(x)\)
Решение:
Функция \(f(x)= e^x \sin(x)\) состоит из произведения двух функций \(y_1=e^x\) - монотонно возрастающая функция и \(y_2=\sin(x)\) - периодическая функция с периодом \(2\pi\), поэтому рассматривать функцию будем на указанном периоде, например на отрезке \([-\pi;\pi]\). Поведение функции на других интервалах будет аналогично.
Схема исследования функции на максимум (экстремум).
1. Находим интервалы монотонности.
Найдем критические (стационарные) точки, для этого найдем первую производную и приравняем ее к нулю $$y' = ( e^x \sin(x))'= e^x \sin(x) + e^x \cos(x) $$ приравняем к 0 $$ e^x \sin(x) + e^x \cos(x) = 0 => \sin(x) + \cos(x) = 0 => $$$$ \sqrt{2} \sin(\frac{\pi}{4}+x) =0 => \frac{pi}{4}+x = \pi n => x = -\frac{\pi}{4} + \pi n$$ функция имеет две критические (стационарные) точки на рассматриваемом интервале $$x_1 = - \frac{\pi}{4}; \quad x_2= \frac{3\pi}{4}$$
2. Находим интервалы монотонности.
Функция имеет две критические точки, они делят рассматриваемый интервал на три интервала монотонности.
интервал \((-\pi; - \frac{\pi}{4})\) найдем значение первой производной в любой точке интервала \(f(- \frac{\pi}{2}) = e^x(\sin(x) + \cos(x)) < 0\), на этом интервале функция убывает.
интервал \((- \frac{\pi}{4}; \frac{3\pi}{4})\) найдем значение первой производной в любой точке интервала \(f(0) = e^x(\sin(x) + \cos(x)) > 0\), на этом интервале функция возрастает.
интервал \(( \frac{3\pi}{4}; \pi)\) найдем значение первой производной в любой точке интервала \(f(\frac{7}{8}\pi) = e^x(\sin(x) + \cos(x)) < 0\), на этом интервале функция убывает.
Экстремумы функции.
Достаточным условием существования экстремума является изменение знака производной при переходе через критическую точку.
для \(x = - \frac{\pi}{4}\): \(\quad - \quad 0 \quad +\), т.е. функция имеет точку минимума с координатами \((- \frac{\pi}{4};-0.32)\)
для \(x = \frac{3\pi}{4}\): \(\quad + \quad 0 \quad -\), т.е. функция имеет точку максимума с координатами \(( \frac{3\pi}{4};7.46)\)
Можно убедиться, что на других интервалах функция будет вести себя аналогично с учетом периода, т.к. функция \(y_1=e^x\) монотонно возрастающая, то значения функции в точках экстремума будут возрастать по модулю.
Т.о. можно записать:
интервалы возрастания \((- \frac{\pi}{4} + 2\pi n; \frac{3\pi}{4} + 2\pi n)\)
интервалы убывания \((- \pi + 2\pi n; -\frac{\pi}{4} + 2\pi n) \cup ( \frac{3\pi}{4} + 2\pi n; \pi + 2\pi n)\)
Экстремумы:
максимумы при : \(x = \frac{3\pi}{4} + 2\pi n\)
минимумы при : \(x = -\frac{\pi}{4} + 2\pi n\)
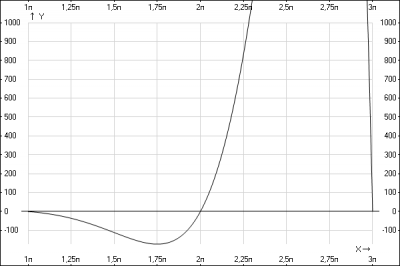
График функции
на отрезке \([-\pi;\pi]\)
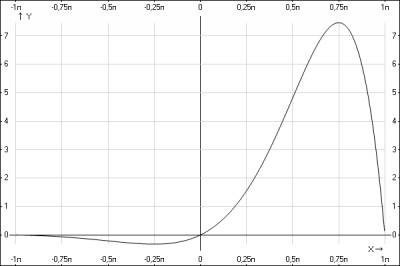
на отрезке \([-3\pi;-\pi]\)
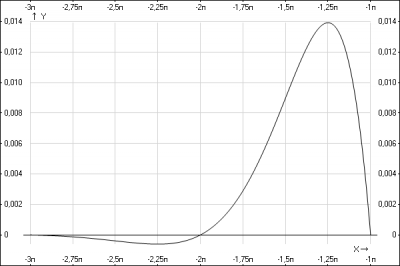
на отрезке \([\pi;3\pi]\)