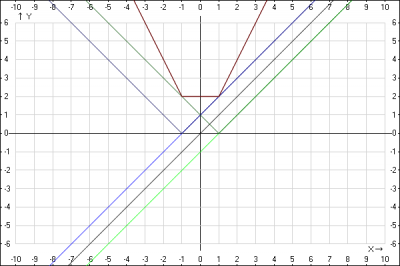
Решение: построим график функции \( y= ||x-1|+|x+1|| \) путем элементарных преобразований
Порядок построения графика функции.
Упрощающий прием построения графиков суммы функций.
а) Если дана сумма функций, то строится графики функций каждой из них.
б) Преобразуем две функции путем сложения соответствующих ординат в одну функцию.
Представим заданную функцию \(y= ||x-1|+|x+1|| = y= |y_1+y_2| \), где \(y_1 = |x-1|, y_2 = |x+1|\)
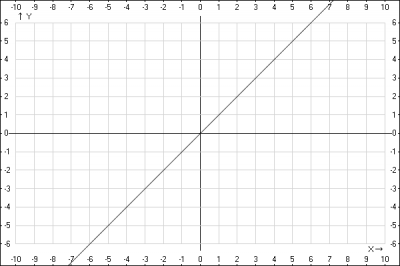
1. Строим график элементной линейной функций \(y= x\)
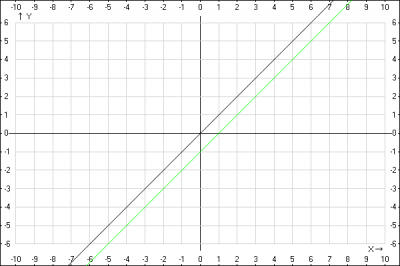
2. Строим график функции \(y = x-1\). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = a+ f(x)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Oy) на \(a\) единиц, если \(a > 0 \) вверх и если \(a < 0 \) вниз.
График функции \(y = x\) переносим на 1 вниз вдоль оси Oy, получаем график функции \( y = x-1 \)
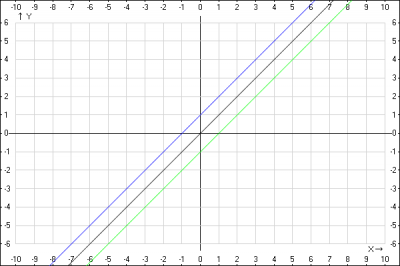
3. Строим график функции \(y = x+1\). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = a+ f(x)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Oy) на \(a\) единиц, если \(a > 0 \) вверх и если \(a < 0 \) вниз.
График функции \(y = x\) переносим на 1 вверх вдоль оси Oy, получаем график функции \( y = x+1 \)
4. Строим график функции \(y = |x-1|; \quad y = |x+1| \). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = |f(x)| \), нужно часть кривой \(y = f(x)\), которая находится ниже оси Ox зеркально отобразить относительно оси Ox.
Зеркально отображаем график функции \(y = x-1 \) относительно оси Ox, получаем график функции \(y = |x-1| \)
Зеркально отображаем график функции \(y = x+1 \) относительно оси Ox, получаем график функции \(y = |x+1| \)
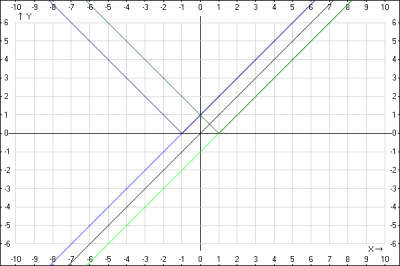
5. Складываем ординаты (y) функций при одинаковых абсциссах (x)