Решение: строим ромб, описанный вокруг окружности с острым углом \(60^0\).
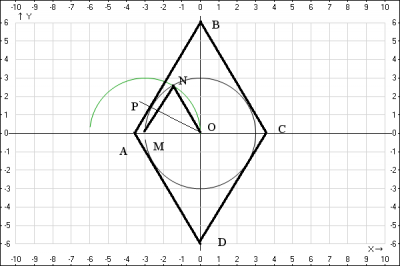
1. Проводим окружность с центром в т.О.
2. Проводим две перпендикулярные прямые через центр окружности AC и BD, на которых лежат диагонали ромба (свойство диагоналей ромба - они перпендикулярны и в точке пересечения делятся пополам).
3. Из любой точки пересечения прямых (например M) строим окружность с там же радиусом и получаем точку пересечения окружностей N.
Соединяем центры окружностей O,M и точку пересечения N. Получился правильный треугольник ΔMNO. Эти построения нужны были для получения угла \(60^0\)
4. Из центра окружности (вершины треугольника O) проводим прямую через середину стороны MN до пересечения с окружностью в т. P (OP - медиана и высота правильного треугольника ).
5. В точке P строим прямую параллельную MN (перпендикулярную OP) до пересечения с прямыми AC и BD получили точки пересечения, которые назовем A и B.
6. Откладываем на прямой AC отрезок OC=OA
7. Откладываем на прямой BD отрезок OD=OB
8. Соединяем все точки.
углы \(\angle N = \angle B = 60^0\)



