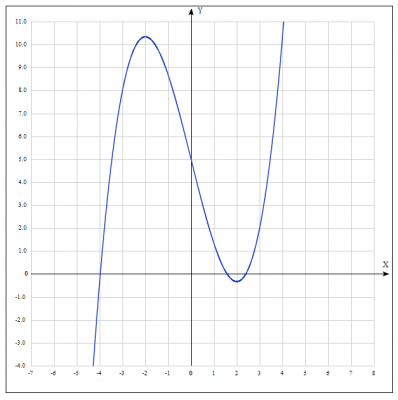
Исследуем функцию \(y = \frac{x^3}{3}-4x+5 \) и построим ее график.
1. Область определения.
Областью определения многочлена является вся область действительных чисел $$D_f=( -\infty; +\infty)$$
2. Точки разрыва функции и их классификация.
Функция не имеет точек разрыва, ОДЗ \(x \in R\).
3. Четность функции.
Проверяем на четность \(f(-x) = \frac{x^3}{3}-4x+5 = \frac{(-x)^3}{3}-4(-x)+5 = - \frac{x^3}{3}+4x+5 \) функция не является ни четной ни не четной, поэтому далее будем исследовать график функции на всем интервале области определения \((- \infty; +\infty)\).
4. Нули функции (точки пересечения с осью Ox). Интервалы знакопостоянства функции.
Нули функции (точка пересечения с осью Ox): приравняем \(y=0\), получим \( \frac{x^3}{3}-4x+5 = 0 => x_1 \approx -3.97 \quad x_2 \approx 1.58 \quad x_3 \approx 2.4 \). Кривая имеет три точки пересечения с осью Ox с координатами \((-3.97;0)\), \((1.58;0)\) и \((2.4;0)\)
Интервалы знакопостоянства функции. На рассматриваемом интервале \(( -\infty; +\infty)\) кривая имеет три точки пересечения с осью Ox , т.е. четыре интервала знакопостоянства
Определим знак функции на этих интервалах
интервал \((-\infty; -3.97)\) найдем значение функции в любой точке \(f(-5) = \frac{x^3}{3}-4x+5 < 0 \), на этом интервале функция отрицательная \(f(x) < 0 \), т.е. находится ниже оси Ox.
интервал \(( -3.97; 1.58)\) найдем значение функции в любой точке \(f(0) = \frac{x^3}{3}-4x+5 > 0 \), на этом интервале функция отрицательная \(f(x) > 0 \), т.е. находится выше оси Ox.
интервал \((1.58; 2.4)\) найдем значение функции в любой точке \(f(2) = \frac{x^3}{3}-4x+5 < 0 \), на этом интервале функция отрицательная \(f(x) < 0 \), т.е. находится ниже оси Ox.
интервал \(( 2.4; +\infty)\) найдем значение функции в любой точке \(f(3) = \frac{x^3}{3}-4x+5 > 0 \), на этом интервале функция отрицательная \(f(x) > 0 \), т.е. находится выше оси Ox.
5. Точки пересечения с осью Oy: приравняем \(x=0\), получим \( \frac{x^3}{3}-4x+5 = 5 \) , т.е кривая пересекает ось Oy в точке с координатами \((0; 5)\)
6. Интервалы монотонности. Экстремумы функции.
Найдем критические (стационарные) точки, для этого найдем первую производную и приравняем ее к нулю $$ y' = ( \frac{x^3}{3}-4x+5)' = x^2-4 $$ приравняем к 0 $$ x^2-4 = 0 => x_1 = -2; \quad x_2 = 2$$ функция имеет две критические (стационарные) точки с координатами \((-2; 10.33)\) и \((2; -0.33)\)
Интервалы монотонности.
Функция имеет две критические точки на интервале ОДЗ \((-\infty; +\infty)\), т.е. две точки возможного экстремума функции. Эта точка делит область определения на три интервала монотонности.
Определим монотонность функции на этих интервалах:
интервал \((-\infty; -2)\) найдем значение первой производной в любой точке интервала \(f'(-3) = x^2-4 > 0\), на этом интервале функция возрастает.
интервал \((-2; 2)\) найдем значение первой производной в любой точке интервала \(f'(0) = x^2-4 < 0\), т.е. на этом интервале функция убывает.
интервал \(( 2; +\infty)\) найдем значение первой производной в любой точке интервала \(f'(4) = x^2-4 > 0\), на этом интервале функция возрастает.
Экстремумы функции.
При исследовании функции получили на интервале ОДЗ одну критическую (стационарную) точку. Определим, является ли она экстремумом. Рассмотрим изменение знака производной при переходе через критическую точку:
точка \(x= -2\) производная меняет знак с \( \quad + \quad 0 \quad - \quad\) - точка максимума, а координаты точки максимума \((-2; 10.33)\).
точка \(x= 2\) производная меняет знак с \( \quad - \quad 0 \quad + \quad\) - точка минимума, а координаты точки максимума \((2; -0.33)\).
7. Интервалы выпуклости и вогнутости. Точки перегиба.
Для нахождения интервалов выпуклости и вогнутости найдем вторую производную функции и приравняем ее к нулю $$y'' = ( x^2-4)' = 2x $$ Приравняем к нулю $$ 2x = 0 => x = 0 $$ Функция имеет одну точу перегиба, которая дели область определения на два интервала выпуклости:
интервал \((-\infty; 0)\) найдем значение второй производной в любой точке \(f''(-1) = 2x < 0 \), на этом интервале вторая производная функции отрицательная \(f''(x) < 0 \) - функция выпуклая вверх (вогнутая).
интервал \(( 0; \infty)\) найдем значение второй производной в любой точке \(f''(1) = 2x > 0 \), на этом интервале вторая производная функции положительная \(f''(x) > 0 \) - функция выпуклая вниз (выпуклая).
Точки перегиба.
В точке \(x = 0 \) вторая производная меняет знак с \( \quad - \quad 0 \quad + \quad\), график функции меняет выпуклость, т.е. это точка перегиба с координатами \(( 0 ;5)\).
8. Асимптоты.
Вертикальная асимптота. График функции не имеет вертикальных асимптот, т.к. ОДЗ \(x \in R\).
Наклонная асимптота.
Для того, чтобы график функции \(у= \frac{x^3}{3}-4x+5 \) при \(x \to \infty\) имел наклонную асимптота \(y = kx+b\), необходимо и достаточно, чтобы существовали два предела $$\lim_{x \to +\infty}=\frac{f(x)}{x} =k $$находим его $$ \lim_{x \to +\infty} ( \frac{x^2}{3}-4+\frac{5}{x}) = \infty => k= \infty $$ и второй предел $$ \lim_{x \to +\infty}(f(x) - kx) = b$$ т.к. \(k = \infty\) - наклонной асимптоты нет.
Горизонтальная асимптота: для того, чтобы существовала горизонтальная асимптота, необходимо, чтобы существовал предел $$\lim_{x \to \infty}f(x) = b$$ найдем его $$ \lim_{x \to -\infty}( \frac{x^3}{3}-4x+5)= -\infty$$$$ \lim_{x \to +\infty}( \frac{x^3}{3}-4x+5)= \infty$$
Горизонтальной асимптота нет
9. График функции.