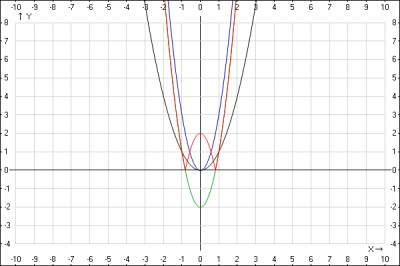
Решение: построим график функции \(y= |3х^2-2|\) путем элементарных преобразований
Порядок построения графика функции.
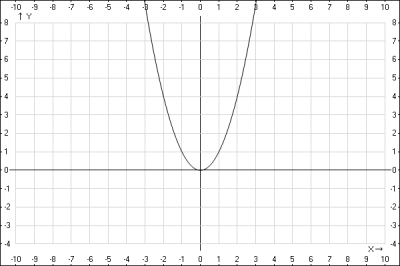
1. Строим график элементной степенной функции \(y= х^2\)
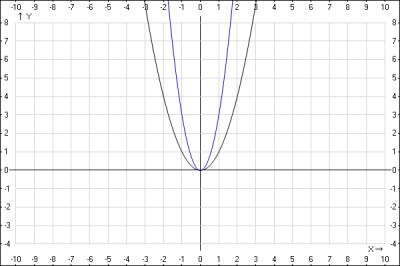
2. Строим график функции \(y = 3х^2\). Элементарное преобразование с деформацией.
Для того, чтобы построить график функции \(y=af(x)\), нужно каждую ординату графика функции \(y = f(x)\) умножить на \(a\).
Ординаты графика функции \(y= х^2\) умножаем на 3 и получаем \(y= 3х^2\), т.к. \(a = 3 > 1\), то график функции растягивается вдоль оси Oy.
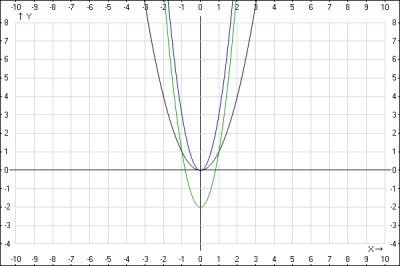
3. Строим график функции \(y = 3х^2 -2\). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = a+ f(x)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Oy) на \(a\) единиц, если \(a > 0 \) вверх и если \(a < 0 \) вниз. График функции \(y = 3x^2\) переносим на 2 вниз вдоль оси Oy, получаем график функции \( y = 3x^2 -2 \)
4. Строим график функции \(y = |3x^2 - 2| \). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = |f(x)| \), нужно часть кривой \(y = f(x)\), которая находится ниже оси Ox зеркально отобразить относительно оси Ox.
График функции \(y = 3x^2 - 2 \), лежащий ниже оси Ox зеркально отображаем относительно этой оси.