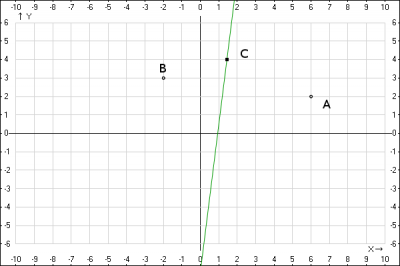
Решение: найдем расстояние между точками, чтобы понять как расположена искомая кривая. Расстояние найдем по формуле \(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \quad (1)\), подставляем координаты точек $$d = \sqrt{(-2-6)^2+(3-2)^2} = \sqrt{65} > \sqrt{12} $$ получили, что кривая находится между точками A и B. Пусть точка C(x;y) принадлежит искомой кривой.
Согласно условия задачи, квадрат расстояние между точками будет равен (согласно формуле (1))
\(AC^2 = (x-6)^2+(y-2)^2\)
\(BC^2 = (x+2)^2+(y-3)^2\)
Согласно условия задачи $$AC^2 = BC^2 + 12$$ подставляем $$(x-6)^2+(y-2)^2 = (x+2)^2+(y-3)^2 + 12 => $$
$$x^2-12x+36+y^2-4x+4 = x^2+4x+4+y^2-6y+9+12 => 14x = 15 => y = 8x - \frac{15}{2}$$
Ответ: линия, квадрат расстояния от которой до точки A больше квадрата расстояния до точки B на 12 это прямая \(y = 8x - \frac{15}{2}\)