Решение: в задании представлены простейшие показательные функции вида \(y = a^x\), где \(a > 0, a \ne 0\). область определения функции \(x \in (-\infty;+\infty)\),
область значения \(y \in (0;+\infty)\),
график функции пересекает вертикальную ось Oy при \(x=0\), т.е. в точке \((0;1)\).
Поведение функции зависит от основания \(a\)
1. при \(a > 1\) функция возрастает, т.к. при росте \(x\), растет \(y\), ось Ox является горизонтальной асимптотой графика функции, к которой график приближается при \(x \to -\infty\)
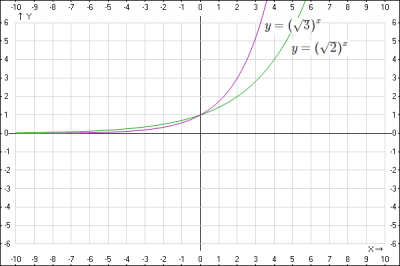
пример функции с основанием \(a > 1\)
\( y = (\sqrt{2})^x\) основание \(a = \sqrt{2} > 1\)
\( y = (\sqrt{3})^x\) основание \(a = \sqrt{3} > 1\)
Построим схематически графики функций.
Основание \(\sqrt{3} > \sqrt{2} \) , график функции с большим основанием расположен ближе к оси Ox при \(x < 0 \), ближе к оси Oy при \(x > 0 \)
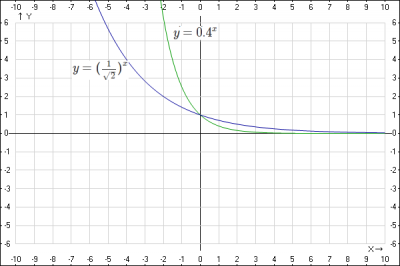
2. при \(a < 1\) функция убывает, т.к. при росте \(x\), уменьшается \(y\), ось Ox является горизонтальной асимптотой графика функции, к которой график приближается при \(x \to +\infty\)
пример функции с основанием \(a < 1\)
\( y = 0.4^x\) основание \(a = 0.4 < 1\)
\( y = (\frac{1}{\sqrt{2}})^x\) основание \(a = \frac{1}{\sqrt{2}} \approx 0.7 < 1\)
Построим схематически графики функций.
Основание \(\frac{1}{\sqrt{2}} > 0.4 \) , график функции с меньшим основанием расположен ближе к оси Ox при \(x > 0 \), ближе к оси Oy при \(x < 0 \)