Решение: Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.
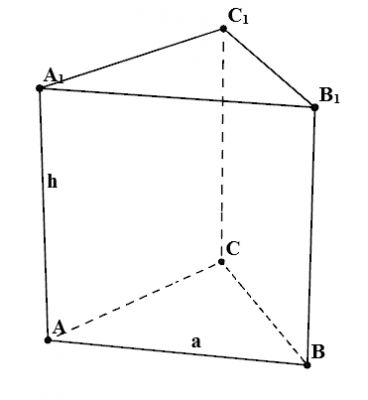
В нашем случае в основании лежит правильный треугольник со стороной \(a\)
Известно, что площадь боковой поверхности \(S_{бок} = 60см^2\), также согласно определения, гранями являются равные прямоугольники со сторонами \(a\) и h = 10 см, т.е. площадь каждой грани \(S_{грани} =10a\), а площадь боковой поверхности \(S_{бок} = 3S_{грани} = 3*10a = 60 => a = 2\). В основании призмы лежит правильный треугольник со стороной \(a= 2\), найдем его площадь по формуле $$S_{основ.}=S_{прав.Δ} = \frac{\sqrt{3}}{4}a^2$$подставляем значение стороны $$S_{основ.} = \frac{\sqrt{3}}{4}2^2 = \sqrt{3}$$
Ответ: площадь основания правильной треугольной призмы равна \(S_{основ.} = \sqrt{3}\)



