составить уравнение поверхности образованной вращением линии $z^2=y^2+\rho$ вокруг оси Оу подобрат

Решение: дано уравнение кривой $z^2=y^2+\rho$
1. Составим уравнение поверхности, образованной вращением линии вокруг оси Oy.
В задании дано уравнение, которое можно рассматривать как проекция фигуры вращения на плоскость zOy, т.е. при x=0.
Т.к. это фигура вращения, то проекция в плоскости xOz  (y = 0 ) это будет окружность, каноническое уравнение которой $x^2+z^2=R^2$ совмещаем два уравнения, получаем при y=0 $x^2+z^2 = \rho$, где $R^2 = \rho$. Итоговое уравнение будет иметь вид $$z^2+x^2=y^2+\rho$$

2. Найдем значение $\rho$ при известных координатах точки, принадлежащей поверхности A(4,5,3).
Подставляем координаты точки в уравнение поверхности $3^2 + 4^2=5^2+\rho => \rho = 0$
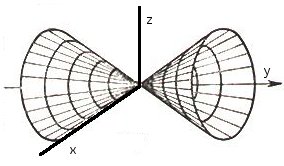
Получили итоговое уравнение искомой кривой $$z^2+x^2=y^2$$  
Рассмотрим проекцию полученного уравнения на плоскость zOy $z^2=y^2 => z = \pm y$ это уравнение прямых $z = y \quad z = -y$, т.е. фигура вращения получена вращением прямых $z = y \quad z = -y$ вокруг оси Oy.

3. Схематический чертеж: