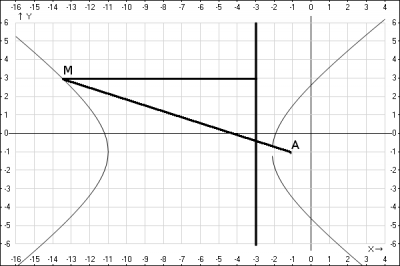
Решение: Рассмотрим рисунок, предположим, что на рисунке искомая кривая. Выберем любую точку на кривой и составим уравнение, согласно условия задачи. Рассмотрим т. M(x;y). Запишем уравнение для этой точки. Расстояние от этой точки до точки A(-1;-1) в декартовой системе координат равно $$S=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$ Подставляем координаты точек и получаем $$S=\sqrt{(x+1)^2+(y+1)^2}$$ В задании говорится о расстоянии от точки кривой до прямой \(x = -3\), которое равно разности координат x точки кривой и прямой, т.е. которое равно \(x+3\). Согласно условия, отношение этих длин равно $$ \frac{\sqrt{(x+1)^2+(y+1)^2}}{x+3} = \frac{5}{4} => \frac{(x+1)^2+(y+1)^2}{(x+3)^2} = \frac{25}{16} =>$$$$ 16(x+1)^2+16(y+1)^2 = 25(x+3)^2 => $$$$ 16x^2+32x+16+16(y+1)^2 = 25x^2+150x+225 => $$$$ 16(y+1)^2 = 9x^2+118x+209 => $$выделим полный квадрат по переменной \(x\), получаем \(9x^2+118x+209 = 9x^2+2*3*\frac{59}{3}x+(\frac{59}{3})^2-(\frac{59}{3})^2+209 =>\) \(= (3x+\frac{59}{3})^2-(\frac{59}{3})^2+209 = 9(x+\frac{59}{9})^2-\frac{1600}{9}\), подставляем $$16(y+1)^2 = 9(x+ \frac{59}{9})^2- \frac{1600}{9} => $$$$ 9(x+\frac{59}{9})^2 - 16(y+1)^2 = \frac{1600}{9} => $$разделим обе части уравнения на число \(\frac{1600}{9}\) $$ 9(x+ \frac{59}{9})^2* \frac{9}{1600} - 16(y+1)^2* \frac{9}{1600} = 1 => $$$$ (x+\frac{59}{9})^2*\frac{81}{1600} - (y+1)^2*\frac{9}{100} = 1 $$ Получили уравнение гиперболы, приведем его к каноническому виду $$ \frac{(x+\frac{59}{9})^2}{(\frac{40}{9})^2} - \frac{(y+1)^2}{(\frac{10}{3})^2} = 1 $$
Строим полученную гиперболу.
Ответ: уравнение искомой кривой - гипербола \( \frac{(x+\frac{59}{9})^2}{(\frac{40}{9})^2} - \frac{(y+1)^2}{(\frac{10}{3})^2} = 1 \)