Рассмотрим рисунок задаче, где \(AM\) - медиана треугольника \(ABC\), а \(AH\) - высота. Разберемся почему рисунок должен бытьт таким, т.е. точка \(H\) лежит между \(B\) и \(M\), а не \(C\) и \(M\). Я разместил высоту ближе к вершине \(D\) так как в условии есть одно указание \(\frac{MH}{BH}=\frac{3}{2}\) т.е. \(MH > BH\), т.е. \(H\) лежит между \(B\) и \(M\) (если бы между \(C\) и \(M\), то \(BH>HM\), а в условии \(MH > BH\) ).
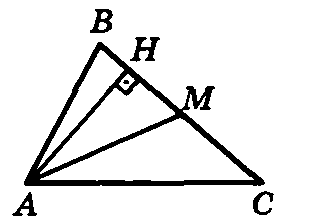
Приступаем к решению. Данная задача на свойство медианы - медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника одинаковой площади \(S_{ΔAMC}=S_{ΔAMB}\), т.е. искомая площадь \(S_{ΔABC} = 2*S_{ΔAMB}\). Т.е для решения задачи будем искать \(S_{ΔAMB}\), которую в свою очередь можно представить как сумма площадей \(S_{ΔAMB} = S_{ΔABH}+S_{ΔAHM}\) при этом \(S_{ΔAHM} = 24\). Т.е. нужно найти \(S_{ΔABH}\). Для ее поиска в условии есть указания \(\frac{MH}{BH}=\frac{3}{2}\), т.е эта два треугольник прямоугольные, у которых общая высота \(AH\), имея связь между основаниями на которые опущена общая высота можно найти связь между площадями. Ищем \(S_{ΔAHM} = \frac{1}{2}AH*HM=24\), а \(S_{ΔABH} = \frac{1}{2}AH*BH\) из условия известно \(\frac{MH}{BH}=\frac{3}{2} =>BH = \frac{2}{3}MH\), подставим в формулу площади $$S_{ΔABH} = \frac{1}{2}AH*BH = \frac{1}{2}AH*\frac{2}{3}MH=$$ где \(\frac{1}{2}AH*HM=24\) подставляем $$S_{ΔABH} = \frac{2}{3}*24 = 16$$ Теперь можно найти и площадь треугольника \(ABC\) $$S_{ΔABC} = 2*S_{ΔAMB} = 2*(S_{ΔABH}+S_{ΔAHM}) = 2*(24+16)=80$$ Ответ: площадь треугольника \(ABC\) \(S_{ΔABC} = 80\).



