Для решения задачи нарисуем произвольный многоугольник и впишем в него окружность. Соединим все вершины с центром окружности и опустим радиус окружности в точку касания. Как известно, радиус, опущенный в точку касания перпендикулярен касательной (стороне многоугольника). Получили рисунок, рассмотрим его.
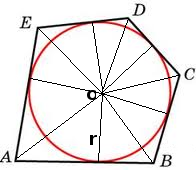
Из рисунка на примере \(ΔABC\) видно, что высота треугольника равна радиусу вписанной окружности и соответственно площадь треугольника можно представить так \(S_{ΔABC} =\frac{1}{2}r*AB\). Из условия задачи известна площадь многоугольника. Представим площадь многоугольника как площадь треугольников с вершиной в центре окружности \(S_{ABCDE}=\frac{1}{2}rAB+\frac{1}{2}rBC+\frac{1}{2}rCD+\frac{1}{2}rDE+\frac{1}{2}rEA\). Т.к. у нас не известно сколько углов в многоугольнике обозначим стороны многоугольника как \(a_1,a_2,a_3, ..... ,a_n\) и запишем предыдущую формулу для площади для произвольного многоугольника $$S_{n}=\frac{1}{2}ra_1 + \frac{1}{2}ra_2 + \frac{1}{2}ra_3 + ... + \frac{1}{2}ra_n = \frac{1}{2}r(a_1 + a_2 + a_3 + ... + ra_n) $$в скобках у нас получилась сумма сторон, а это как раз и есть периметр многоугольника $$P=a_1+a_2+a_3+...+a_n$$ из условия известно, что \(P=15\). Поставим это значение в формулу $$S_n=\frac{1}{2}r(a_1 + a_2 + a_3 + ... + ra_n) = \frac{1}{2}r*15=7,5 =>r=1$$Ответ: радиус окружности вписанной в многоугольник равен \(r=1\)



