Відомі вершини трикутника АВС.
Знайти:
1) рівняння висоти АЕ
2) рівняння медіани СК
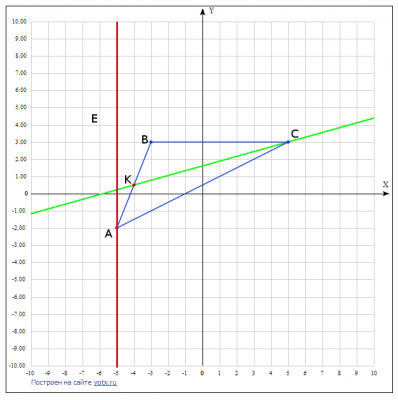
Трикутник показати на рисунку
А(-5;-2), В(-3;3), С(5;3)
1. Рівняння висоти CD
Рівняння виду \(Ax + By + C = 0 \) - називається загальним рівнянням прямої на площині, тоді вектор \(s = (-B; A) \) - і всякий ненульовий вектор, з ним колінеарний, називається напрямних вектором цієї прямої., тоді вектор \(N = (A; B) \) - перпендикулярний цій прямій і цей вектор є нормаллю до цієї прямої. Рівняння прямої \(Bx-Ay + C_2 = 0 \) - рівняння прямої, перпендикулярної прямої \(Ax + By + C = 0 \).
У завданні дані координати всіх точок, тому знайдемо рівняння прямої \(BC \), а потім висоти. Рівняння прямої будемо шукати як рівняння прямої, що проходить через дві задані точки за формулою $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) $$ або з прив'язкою до коефіцієнтів загального рівняння прямої \( \frac{x-x_1}{- B} = \frac{y-y_1}{A} \) Підставляємо координати точок В (-3; 3), С (5; 3) $$ \frac{x + 3}{5 + 3} = \frac{y-3}{3-3} = > \frac{x + 3}{8} = \frac{y-3}{0} $$ Завдання істотно спростилася, тому вектор направляючої має координати \(s = (8; 0) \), тобто пряма \(BC \) паралельна осі Ox і її рівняння \(y = 3 \). Тоді висота, через точку А(-5; -2), паралельна осі Oy матиме рівняння \(x = -5 \), перевіримо це.
Коефіцієнти загального рівняння прямої рівні \(A = 0; B = -8 \). Отримали рівняння прямої \(BC \): \(0 * x-8y + C = 0 \).
Рівняння висоти отримуємо шляхом заміни коефіцієнтів перед \(x \) і \(y \) і знака перед однією з змінних, тобто отримуємо рівняння висоти \(8x + 0y + C = 0 \) Підставляємо координати відомої точки прямої А (-5; -2), отримуємо \(8 * (- 5) + C = 0 => C = 40 \) , рівняння висоти $$ 8x + 40 = 0 => x = -5 $$
Відповідь: рівняння висоти BC: \(x = -5 \)
2. Рівняння медіани CK;
Рівняння медіани CK.
Для знаходження медіани CK є координата однієї точки С (5; 3), а координати другої точки прямої K знайдемо як координати середини відрізка \(AB \), де А(-5; -2), В(-3; 3) за формулою \(K ( \frac{x_A + x_B}{2} ; \frac{y_A + y_B}{2}) \) => \(K ( \frac{-5-3}{2}; \frac{-2 + 3}{2}) \) => \(K (-4; \frac{1}{2}) \)
Знаходимо рівняння прямої \(CK \) за формулою рівняння прямої, що проходить через дві задані точки \(C \) і \(K \) рівняння (1) $$ \frac{x-5}{- 4-5} = \frac{y-3}{ \frac{1}{2} -3} => y = \frac{5}{18} x + \frac{29}{18} $$
Відповідь : рівняння медіани \( y = \frac{5}{18} x + \frac{29}{18} \)



