Дано уравнение кривой второго порядка \(36х^2 -4у^2 + 72х - 32у + 116=0\)
Записать уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$36х^2 -4у^2 + 72х - 32у + 116=0=> 4(9x^2+18x-y^2-8y+29)=0 => $$для упрощения расчетов, разделили все члены многочлена на общий делитель 4 $$ 9x^2+18x-y^2-8y+29=0 => 9(x^2+2x)-(y^2+2*4y)+29=0 =>$$дополняем члены в скобках до полного квадрата$$ 9(x^2+2x+1-1)-(y^2+2*4y+16-16)+29=0 => $$$$ 9((x+1)^2-1)-((y+4)^2-16)+29=0 => 9(x+1)^2-9-(y+4)^2+16+29=0 => $$$$ 9(x+1)^2-(y+4)^2=-36 => \frac{(x+1)^2}{4}-\frac{(y+4)^2}{36}=-1$$ Получили уравнение гиперболы. Каноническое уравнение гиперболы $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1$$ Смотрим на знак минус (-1), это указывает на то, что ось Oy - действительная ось, а ось Ox - мнимая. Из уравнения получаем значения полуосей \(a = 2; b=6\).
Координаты вершин (точек пересечения с действительной осью). Приравниваем \(x+1=0 => x=-1\), получаем \(0-\frac{(y+4)^2}{36}=-1 => y_1=-10;y_2=2\) \(A_1(-1;-10);A_2(-1;2)\).
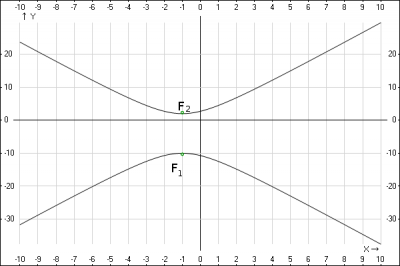
Координаты фокусов: координаты фокусов для уравнения гиперболы в каноническом виде следующие \(F_1(0;-c);F_2(0;+c)\), где \(c= \sqrt{a^2+b^2} = \sqrt{36+4} = 2\sqrt{10}\). Мы получили уравнение гиперболы сдвинутое относительно осей. Введем обозначение \(x' = x+1;y'=y+4\), получили систему координат \(x'y'\). Подставим эти координаты в полученное уравнение \(\frac{(x')^2}{4}-\frac{(y')^2}{36}=-1\). Координаты фокусов \(F_1(0;-c);F_2(0;+c)\) соответствуют системе координат \(x'y'\), а нам нужны координаты в системе \(xy\). Перейдем к исходной системе координат \(xy\), для этого проведем преобразования \(x' = x+1;y'=y+4 => x = x'-1;y=y'-4\), т.е. чтобы получить координаты фокусов в исходной системе координат нужно от новой координаты \(x'\) вычесть 1,а от \(y'\) вычесть 4, тогда координаты фокусов получим \(F_1(0;-c);F_2(0;+c)\) - новая система координат, а \(F_1(0-1;-c-4);F_2(0-1;+c-4)\) - в исходной системе координат. Подставляем значение \(c\) - фокусное расстояние и получаем искомые
координаты фокусов \(F_1(-1;-2\sqrt{10}-4);F_2(-1;2\sqrt{10}-4)\)
Эксцентриситет - характеристика формы гиперболы. Уравнение эксцентриситета $$\epsilon = \frac{c}{b} = \frac{\sqrt{a^2+b^2}}{b}$$ подставляем данные $$\epsilon = \frac{\sqrt{36+4}}{6} = \frac{\sqrt{10}}{3} $$
Рисунок кривой: