Решение:
Воспользуемся определением выпуклого четырехугольника:
четырехугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую его сторону.
В данном случае алгоритм будет следующий.
1. Находим уравнения сторон.
2. Берем одну из сторон и рассчитываем расстояние от двух других вершин до стороны с учетом знака (находим отклонение). Если знак одинаковый, то вершины лежат в одной полуплоскости, если разные, то в разных полуплоскостях.
План решения задачи:
1. находим уравнения всех сторон.
Т.к. в задаче даны последовательные координаты сторон, будем брать последовательно по две точки и находить уравнение прямой по формуле уравнения прямой, проходящей через две заданные точки \(\frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}\)
Уравнение сторон:
AB: \(\frac{x+3}{-1+3} = \frac{y-5}{4-5} => y = 3,5 - \frac{1}{2}x\)
BC: \(\frac{x+1}{7+1} = \frac{y-4}{-1-4} => y = \frac{27}{8} - \frac{5}{8}x\)
CD: \(\frac{x-7}{2-7} = \frac{y+1}{9+1} => y = 13 - 2x\)
AD: \(\frac{x+3}{2+3} = \frac{y-5}{9-5} => y = \frac{37}{5} + \frac{4}{5}x\)
2. Находим отклонение
Наносим точки и прямые на декартовую систему координат.
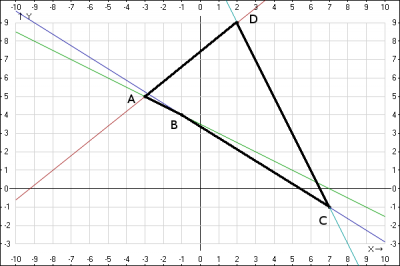
Подозрение вызывает только точка B, поэтому рассмотрим сторону BC и две точки A и D
Найдем отклонение от точки до прямой по формуле \( \sigma = \frac{Ax_0+by_0+C}{\sqrt{A^2+B^2}}\), где \(Ax_0+by_0+C = 0\) - уравнение прямой в общем виде, а \(x_0;y_0\) - координаты точки.
Приведем уравнение прямой \(BC\) - к общему виду \(y = \frac{27}{8} - \frac{5}{8}x => 5x + 8y - 27 =0\)
Рассчитаем отклонение для точки
\(A(-3;5)\), получаем \(\sigma = \frac{5*(-3) + 8*5 - 27}{\sqrt{5^2+8^2}} = - \frac{2}{\sqrt{89}}\)
\(D(2;9)\), получаем \(\sigma = \frac{5*2 + 8*9 - 27}{\sqrt{5^2+8^2}} = \frac{55}{\sqrt{89}}\)
Получили разные знаки, т.к. точки лежат в разных полуплоскостях, т.е. четырехугольник не является выпуклым (он вогнутый)
Ответ: четырехугольник не является выпуклым (вогнутый).



