Дано уравнение кривой второго порядка \(3x^2+3y^2+6x-4y-1=0\)
Записать уравнение кривой второго порядка в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$3x^2+3y^2+6x-4y-1=0 =>$$$$ 3(x^2+2x)+3(y^2- \frac{4}{3}y)-1=0=> $$$$ 3(x^2+2x+1-1)+3(y^2-2* \frac{2}{3}y+ \frac{4}{9}- \frac{4}{9})-1=0 => $$$$ 3((x+1)^2-1)+3((y- \frac{2}{3})^2-\frac{4}{9})-1=0 =>$$$$ 3(x+1)^2-3+3(y-\frac{2}{3})^2-\frac{4}{3}-1=0 => $$$$ 3(x+1)^2+3(y-\frac{2}{3})^2-\frac{16}{3}=0$$$$ 3(x+1)^2+3(y-\frac{2}{3})^2 = \frac{16}{3} =>$$$$ (x+1)^2+(y-\frac{2}{3})^2 = \frac{16}{9}$$ Получили уравнение окружности. Каноническое уравнение окружности $$x^2+y^2=r^2$$ Из полученного уравнения следует, что это окружность с центром \(O(-1;\frac{2}{3})\) и радиусом \(r = \frac{4}{3}\)
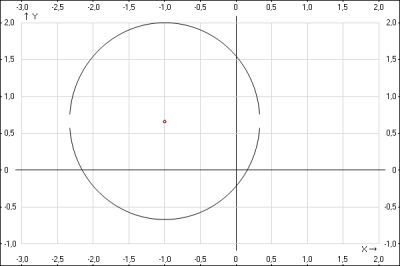
Рисунок кривой: