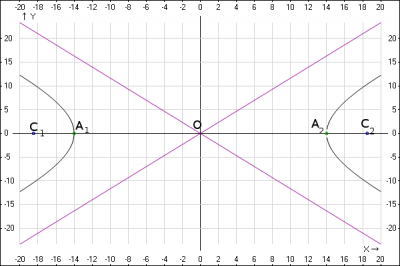
Решение:
дано уравнение гиперболы \(\frac{x^2}{A}-\frac{y^2}{B} = 1\), т.к. знак минус стоит перед переменной \(y\), действительная ось - ось Ox, мнимая ось - ось Oy. Вершины гиперболы лежат га ось Ox симметрично относительно начала координат.
1. Найдем полуоси гиперболы
Каноническое уравнение гиперболы имеет вид $$\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$$ где a и b - полуоси гиперболы, т.е. $$a = \sqrt{A} = \sqrt{196} = 14$$$$b = \sqrt{B} = \sqrt{144} = 12$$
Ответ: полуоси гиперболы равны \(a=14; b=12\)
2.Найдем координаты вершин гиперболы:
Вершины гиперболы - точки пересечения гиперболы с действительной осью. Действительная ось -ось Ox и гипербола симметрична относительно оси Oy, поэтому координаты вершин \(A_1(-a;0);A_2(a;0)\), где \(a = 14\) - действительная полуось.
Ответ: координаты вершин \(A_1(-14;0);A_2(14;0)\)
3.Найдем координаты фокусов:
Для нахождения координат фокусов, воспользуемся соотношением, связывающим полуоси и фокусное расстояние \(c^2 = a^2+b^2\), подставляем значения \(c^2 = 14^2+12^2 => c =2\sqrt{85}\). Координаты фокусов для гиперболы, заданной в каноническом фиде следующие \(F_1(-c;0);F_2(c;0)\)
Ответ: координаты фокусов \(F_1(-2\sqrt{85};0);F_2(2\sqrt{85};0)\)
4.Найдем эксцентриситет гиперболы:
Эксцентриситет будем находить по формуле \(\epsilon=\frac{c}{a}\), подставляем данные \(\epsilon=\frac{2\sqrt{85}}{144} = \frac{\sqrt{85}}{72}\)
Ответ: эксцентриситет гиперболы равен \(\epsilon = \frac{\sqrt{85}}{72}\)
5.Найдем асимптоты гиперболы:
Уравнения асимптот имеют вид \(y = \pm \frac{b}{a}x\). Подставляем данные и получаем две асимптоты \(y = \frac{7}{6}x; y = -\frac{7}{6}x\)
Ответ: уравнения асимптот гиперболы \(y = \frac{7}{6}x; y = -\frac{7}{6}x\)
6. График гиперболы