Решение: рассмотрим два случая
1. действительная ось симметрии гиперболы- ось Ox.
Тогда каноническое уравнение гиперболы будет иметь вид $$\frac{x^2}{a^2} - \frac{y^2}{b^2}=1$$ Согласно условия задачи действительная ось равна \(2a = 5 => a=2,5\). Известно, что вершина делит (имеет координаты (a;0)) расстояние между фокусом (координаты (c;0)) и центром (симметрии - точка О(0;0)) на две равные части, т.е. \(c = 2a => c=5\). Полуоси a,b и фокусное расстояние связаны соотношением $$c^2 = a^2+b^2 => 5^2 = 2,5^2 + b^2 => b^2 = 18,75 $$ Подставляем полученные данные в канонической уравнение гиперболы, получаем $$\frac{x^2}{6,25} - \frac{y^2}{18,75}=1$$
2. действительная ось симметрии гиперболы - ось Oy.
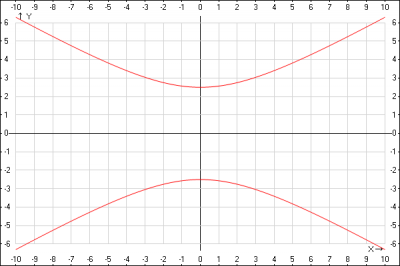 Проведя аналогичные рассуждения, получим каноническое уравнение гиперболы $$\frac{y^2}{6,25} - \frac{x^2}{18,75}=1$$
Проведя аналогичные рассуждения, получим каноническое уравнение гиперболы $$\frac{y^2}{6,25} - \frac{x^2}{18,75}=1$$



