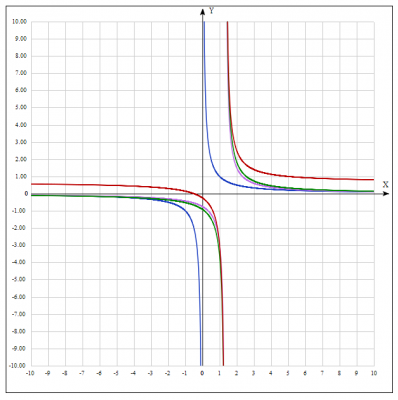
Решение: построим график функции \( y= \frac{2x+1}{3x-4}\) путем элементарных преобразований
Порядок построения графика функции.
1. Проведем преобразования.
Преобразуем уравнение функции, приведем его к одной из элементарных функций (в данном случае к функции - гипербола \(y = \frac{1}{x}\).
Выделим целую часть в числителе $$ y = \frac{2x+1}{3x-4} = \frac{2}{3} \frac{x+\frac{1}{2}}{x-\frac{4}{3}} = $$$$ = \frac{2}{3} \frac{x- \frac{4}{3}+\frac{4}{3}+\frac{1}{2}}{x-\frac{4}{3}} = \frac{2}{3}[ 1 + \frac{\frac{4}{3}+\frac{1}{2}}{x-\frac{4}{3}}] = $$$$ = \frac{2}{3}[ 1 + \frac{11}{6(x-\frac{4}{3})}] = \frac{2}{3} + \frac{11}{9(x-\frac{4}{3})}$$ Получили функцию, которую будем строить $$ y = \frac{2}{3} + \frac{11}{9(x-\frac{4}{3})}$$
2. Строим график элементной функции \(y = \frac{1}{x}\) - гипербола.
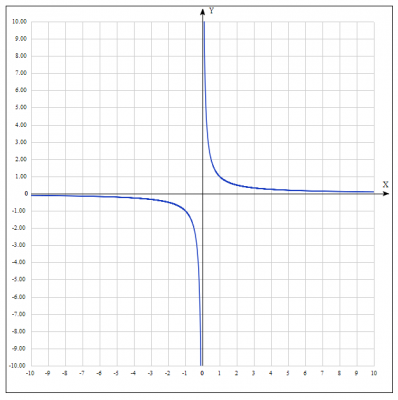
3. Строим график функции \(y = \frac{1}{x-\frac{4}{3}}\). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = f(x+a)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси абсцисс (Ox) на \(a\) единиц, если \(a > 0 \) влево и если \(a < 0 \) вправо. Рассмотрим график функции \(y = \frac{1}{x - \frac{4}{3}}\), получили \(a = - \frac{4}{3}\) переносим график функции \(y = \frac{1}{x}\) на \( \frac{4}{3}\) вправо, получаем график функции \( y = \frac{1}{x - \frac{4}{3}} \).
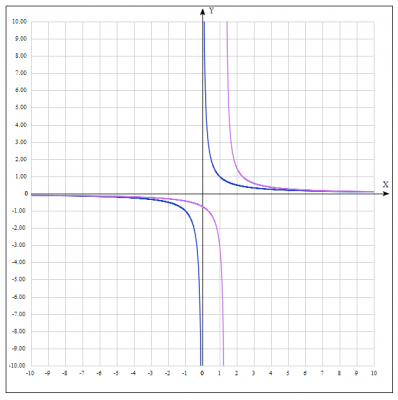
4. Строим график функции \(y = \frac{11}{9(x-\frac{4}{3})}\). Элементарное преобразование с деформацией.
Для того, чтобы построить график функции \(y=af(x)\), нужно каждую ординату графика функции \(y=f(x)\) умножить на \(a\).
Если \(a > 1\), то график функции растягивается вдоль оси Oy.
Если \(a < 1\), то график функции сжимается вдоль оси Oy.
Ординаты графика функции \( y = \frac{1}{x - \frac{4}{3}} \) умножаем на \( \frac{11}{9}\) и получаем \(y = \frac{11}{9(x-\frac{4}{3})}\), т.к. \(a = \frac{11}{9} > 1\), то график функции растягивается вдоль оси Oy.
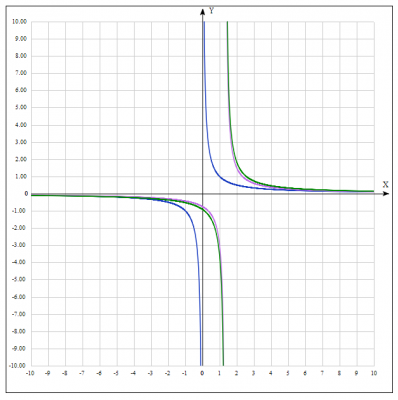
5. Строим график функции \( y = \frac{2}{3} + \frac{11}{9(x-\frac{4}{3})}\). Элементарное преобразование без деформации.
Для того, чтобы построить график функции \(y = a+ f(x)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Oy) на \(a\) единиц, если \(a > 0 \) вверх и если \(a < 0 \) вниз. График функции \(y = \frac{11}{9(x-\frac{4}{3})}\) переносим на \(\frac{2}{3}\) вверх вдоль оси Oy, получаем график функции \( y = \frac{2}{3} + \frac{11}{9(x-\frac{4}{3})}\) .