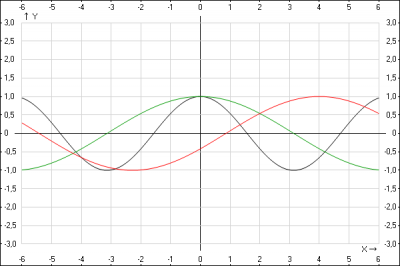
Решение: построим график функции \(y= \cos(\frac{x}{2}-2)\) путем элементарных преобразований
Порядок построения графика функции.
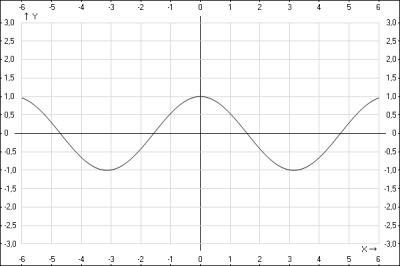
1. Строим график элеменой тригонометрической функции \(y = \cos(x)\)
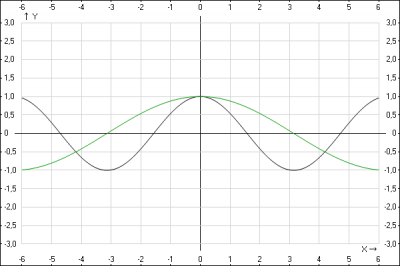
2. Строим график функции \(y = \cos(\frac{x}{2})\)
Для того, чтобы построить график функции \(y = f(ax)\), \(a > 0\), нужно абсциссы ( координаты \(x)\) всех точек графика функции \(y = f(x)\) уменьшить по абсолютной величине в \(a\) раз, если \(a > 1\) и увеличить в \(\frac{1}{a}\) раз, если \(0 < a < 1\). Т.е. График функции расстягивается при \(0 < a < 1\) вдоль оси Ox и сжимается при \(a > 1\) вдоль оси Ox.
В задании \(a = \frac{1}{2} < 1\), т.е. график функции растянется в 2 раза вдоль оси Ox
3. Строим график функции \(y = \cos(\frac{x}{2} -2)\)
Для того, чтобы построить график функции \(y = f(x+a)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Ox) на \(a\) единиц, если \(a > 0 \) влево и если \(a < 0 \) вправо. График функции \(y = \cos(\frac{x}{2})\) переносим на \(2\) вправо вдоль оси Ox, получаем график функции \(y = \cos(\frac{x}{2}-2)\)