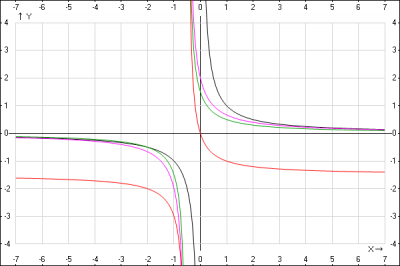
Решение: построим график функции \(y=-\frac{3x}{2x+1}\) путем элементарных преобразований
Порядок построения графика функции.
Проведем алгебраические преобразования
Функция \(y=-\frac{3x}{2x+1}\) - алгебраическая дробь, выделим целую часть$$y=-\frac{3x}{2x+1} =- \frac{3}{2}\frac{x}{x+\frac{1}{2}} = $$$$ = -\frac{3}{2}\frac{x+\frac{1}{2} - \frac{1}{2}}{x+\frac{1}{2}} = -\frac{3}{2} +\frac{\frac{3}{4}}{x+\frac{1}{2}}$$ Получили уравнение гиперболы, построим график функции.
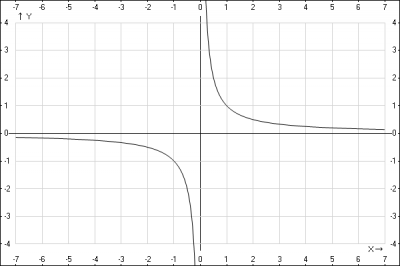
1. Строим график функции \(y = \frac{1}{x}\)
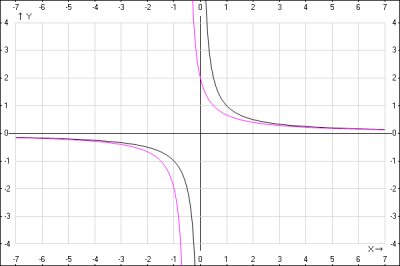
2. Строим график функции \(y = \frac{1}{x+\frac{1}{2}}\)
Для того, чтобы построить график функции \(y = f(x+a)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси абсцисс (Ox) на \(a\) единиц, если \(a > 0 \) влево и если \(a < 0 \) вправо. График функции \(\frac{1}{x}\) переносим на \(\frac{1}{2}\) влево, получаем график функции \(\frac{1}{x+\frac{1}{2}}\)
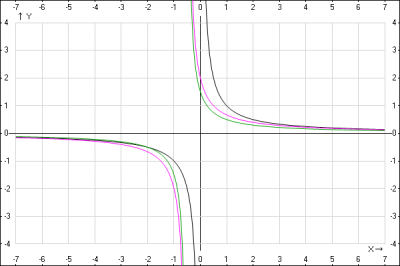
3. строим график функции \(y = \frac{\frac{3}{4}}{x+\frac{1}{2}}\)
Для того, чтобы построить график функции \(y = Af(x)\), нужно ординаты \((y)\) всех точек графика функции \(y = f(x)\) увеличить по абсолютной величине в \(A\) раз (умножить). В нашем случае \(A = \frac{3}{4}\), т.е. каждое значение \(y\) умножаем на \(\frac{3}{4}\).
4. строим график функции \(y = -\frac{3}{2} +\frac{\frac{3}{4}}{x+\frac{1}{2}}\)
Для того, чтобы построить график функции \(y = a+ f(x)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Oy) на \(a\) единиц, если \(a > 0 \) вверх и если \(a < 0 \) вниз. График функции \(y = \frac{1}{x+\frac{1}{2}}\) переносим на \(\frac{3}{2}\) вниз вдоль оси Oy, получаем график функции \(y = -\frac{3}{2} +\frac{1}{x+\frac{1}{2}}\)