Дано: уравнение кривой второго порядка \( 4x^2-9y^2-32x-36y+64=0 \)
1. Запишем уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$4x^2-9y^2-32x-36y+64=0 => $$$$ 4(x^2-8x)-9(y^2+4y)+64=0 =>$$ дополняем члены в скобках до полного квадрата$$ 4(x^2-2*4x+16-16)-9(y^2+4y+4-4)+64=0 => $$$$4(x-4)^2 -4*16 -9(y+2)^2+4*9+64=0 =>$$$$ 4(x-4)^2 -9(y+2)^2+36=0 => $$$$ 9(y+2)^2- 4(x-4)^2 =36 => $$ разделим обе части уравнения на 36 $$ \frac{(y+2)^2}{4} - \frac{(x-4)^2}{9} =1 => \quad (1)$$ Получили уравнение гиперболы.
Рассмотрим каноническое уравнение гиперболы $$ \frac{y^2}{b^2} -\frac{x^2}{a^2} = 1$$ знак минус стоит перед переменной x, это означает, что действительная ось - ось Oy, мнимая ось - ось Ox. Вершины гиперболы лежат га ось Oy симметрично относительно начала координат.
Для того, чтобы привести уравнение (1) к каноническому виду введем новые координаты \(x'=x-4;y'=y+2\), подставляем в уравнение (1) и получаем каноническое уравнение гиперболы в новой системе координат (x';y'), которая смещена относительно базовой системы координат на по оси Оx вправо на 4 и по оси Оy вниз на 2, получаем $$ \frac{(y')^2}{4} - \frac{(x')^2}{9} =1 $$
2. Найдем полуоси гиперболы:
Каноническое уравнение гиперболы имеет вид \( \frac{y^2}{b^2} -\frac{x^2}{a^2} = 1 \), где a и b - полуоси гиперболы, т.е. \( a=3; \quad b=2\),
\(a =3 \) - мнимая полуось
\(b = 2 \) - действительная полуось
Ответ: полуоси гиперболы равны \(a= 3;\quad b=2 \)
3. Найти координаты вершин гиперболы.
Вершины гиперболы - точки пересечения гиперболы с действительной осью. Действительная ось -ось Oy и гипербола симметрична относительно оси Ox, поэтому координаты вершин \(A_1(0;-b);A_2(0; b)\), где \( b=2 \) - действительная полуось.
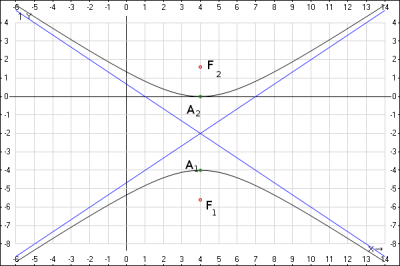
Данные координаты для системы координат \((x';y')\), возвращаемся к базовым координатам \( x'=x-4;y'=y+2 => x=x'+4;y=y'-2\), координаты вершин в базовой системе координат \(A_1(4;-b-2);A_2(4; b-2)\), получаем \(A_1(4;-4);A_2(4; 0)\)
Ответ: координаты вершин в базовой системе координат \(A_1(4;-4);A_2(4; 0)\)
4.Найдем координаты фокусов гиперболы:
Для нахождения координат фокусов, воспользуемся соотношением, связывающим полуоси и фокусное расстояние \(c^2=a^2+b^2\), подставляем значения \(c^2= 3^2+2^2 => c = \sqrt{13}\). Координаты фокусов для гиперболы, заданной в каноническом фиде следующие с действительной осью Oy \(F_1(0;-c);F_2(0;c)\)
Данные координаты для системы координат \((x';y')\), возвращаемся к базовым координатам \( x'=x-4;y'=y+2 => x=x'+4;y=y'-2\), координаты фокусов в базовой системе координат \(F_1(4;-c-2);F_2(4; c-2)\), получаем \(F_1(4;-\sqrt{13}-2);F_2(4; \sqrt{13}-2)\)
Ответ: координаты фокусов гиперболы в базовой системе координат \(F_1(4;-\sqrt{13}-2);F_2(4; \sqrt{13}-2)\)
5.Найдем асимптоты гиперболы:
Уравнения асимптот имеют вид \(y = \pm \frac{b}{a}x\). Подставляем данные и получаем две асимптоты в новой системе координат \( y' =\frac{2}{3}x'; \quad y' =−\frac{2}{3}x'\)
Данные координаты для системы координат \((x';y')\), возвращаемся к базовым координатам \( x'=x-4;y'=y+2 \), уравнение асимптот будут иметь вид, \( y+2=\frac{2}{3}(x-4); \quad y+2 =−\frac{2}{3}(x-4) => y = \frac{2}{3}x - \frac{14}{3} \quad \) \( y = -\frac{2}{3}x + \frac{2}{3}\)
Ответ: уравнения асимптот гиперболы \( y = \frac{2}{3}x - \frac{14}{3} \quad y = -\frac{2}{3}x + \frac{2}{3}\)
6. Построить рисунок: