Решение: вспомним геометрический смысл определенного интеграла.
Если \(f(x)\) непрерывна и положительна на [a, b], то интеграл \(\int_a^bf(x)dx\) представляет собой площадь криволинейной трапеции, ограниченной линиями \(y = 0, x = a, x = b, y = f(x) \)
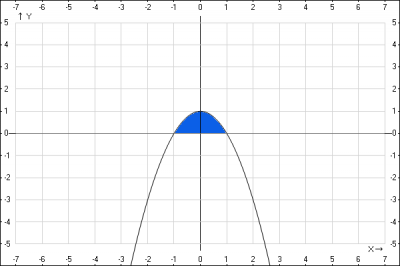
В нашей задаче \(y = f(x)\) - парабола \(y =-x^2+1\) , т.е. нужно найти площадь заштрихованной фигуры, которая равна $$S = \int_{-1}^1(-x^2+1)dx = $$ применим формулу формулу Ньютона-Лейбница \( \int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a) \), получим $$ = -\frac{1}{3}x^3 + x|_{-1}^1 = -\frac{1}{3} + 1 - (-\frac{1}{3}(-1)^3 - 1) = -\frac{1}{3} + 1 - \frac{1}{3} + 1 = \frac{4}{3}$$
Ответ: площадь фигуры равна \(S = \frac{4}{3}\)



