Задание: Найти центр и радиус окружности \(x^2+y^2+6x-14y+26=0\)
Решение: для решения задачи найдем каноническое уравнение окружности $$(x-a)^2 +(y-b)^2 = r^2$$ где точка с координатами \((a,b)\) - центр окружности.
Каноническое уравнение будем получать методом выделения полного квадрата
$$x^2+y^2+6x-14y+26=0 => x^2+2*3x + y^2-2*7y+26=0 =>$$применим формулу квадрата суммы \((a+b)^2 = a^2+2ab+b^2\)$$x^2+2*3x +9-9+ y^2-2*7y+49-49+26=0 => (x+3)^2 - 9+ (y-7) -49+26=0 =>$$$$(x+3)^2 + (y-7)^2 = 32 => (x+3)^2 + (y-7)^2 = (4\sqrt{2})^2$$
Ответ: центр окружности находится в точке с координатами \((-3;7)\), радиус окружности \(r = 4\sqrt{2}\)
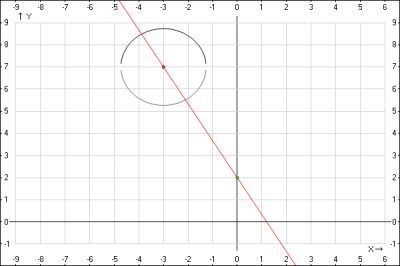
Задание: написать уравнение прямой , проходящей через центр окружности \((-3;7)\) и точку пересечения прямой \(3x-4y+8=0\) с осью Oy
Точка пересечения прямой \(3x-4y+8=0\) с осью Oy имеет координаты \((0;y)\), т.е. подставляем в уравнение значение \(x =0\) и находим \(y\), получаем $$3*0-4y+8=0 => y = 2$$ Получили две точки, через которые проходит прямая. Применим формулу уравнения прямой, проходящей через две заданные точки, в нашем случае \((-3;7)\), \((0;2)\) $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$$ подставляем координаты точек $$\frac{x+3}{0+3} = \frac{y-7}{2-7} => y = 2 -\frac{5}{3}x$$
Ответ: уравнение прямой \(y = 2 -\frac{5}{3}x \)